题目内容
已知函数f（x）=-
x3+2ax2+3x（a＞0）的导数f′（x）的最大值为5，则在函数f（x）图象上的点（1，f（1））处的切线方程是（ ）
| 2 |
| 3 |
| A、3x-15y+4=0 |
| B、15x-3y-2=0 |
| C、15x-3y+2=0 |
| D、3x-y+1=0 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求导数，利用导数f′（x）的最大值为5，求出a的值，根据导数的几何意义求出切线的斜率，切点的坐标，从而可求方程．
解答：
解：∵f（x）=-
x3+2ax2+3x，
∴f′（x）=-2x2+4ax+3=-2（x-a）2+2a2+3，
∵导数f′（x）的最大值为5，
∴2a2+3=5，
∵a＞0，
∴a=1，
∴f′（1）=5，f（1）=
，
∴在函数f（x）图象上的点（1，f（1））处的切线方程是y-
=5（x-1），即15x-3y-2=0．
故选：B．
| 2 |
| 3 |
∴f′（x）=-2x2+4ax+3=-2（x-a）2+2a2+3，
∵导数f′（x）的最大值为5，
∴2a2+3=5，
∵a＞0，
∴a=1，
∴f′（1）=5，f（1）=
| 13 |
| 3 |
∴在函数f（x）图象上的点（1，f（1））处的切线方程是y-
| 13 |
| 3 |
故选：B．
点评：本题主要考查了利用导数研究曲线上某点切线方程，解题的关键注意过某点和在某点的区别，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=|log2（x-1）|-（
）x有两个零点x1，x2，则（ ）
| 1 |
| 3 |
| A、x1x2＜1 |
| B、x1x2＞x1+x2 |
| C、x1x2=x1+x2 |
| D、x1x2＜x1+x2 |
若集合A={y|0≤y＜2}，B={x|-1＜x＜1}，则A∩（∁RB）=（ ）
| A、{x|0≤x≤1} |
| B、{x|1≤x＜2} |
| C、{x|-1＜x≤0} |
| D、{x|0≤x＜1} |
已知集合 A={0，1，2，3}，集合 B={x∈N||x|≤2}，则A∩B=?（ ）
| A、{ 3 } |
| B、{0，1，2} |
| C、{ 1，2} |
| D、{0，1，2，3} |
已知点P（a，b）与点Q（1，0）在直线2x+3y-1=0的两侧，且a＞0，b＞0，则
的取值范围是（ ）
| a-1 |
| b |
| A、（-∞，-3） | ||
B、(-
| ||
| C、（3，+∞） | ||
D、(0，
|
设复数z=
（i为虚数单位），z的共轭复数为
，则在复平面内i
对应当点的坐标为（ ）
| 2 |
| -1-i |
. |
| z |
. |
| z |
| A、（1，1） |
| B、（-1，1） |
| C、（1，-1） |
| D、（-1，-1） |
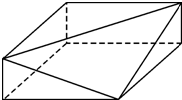某几何体的直观图如图所示，该几何体的主（正）视图和左（侧）视图都正确的是（ ）
