题目内容
已知x、y均为正值,且满足x+2y+xy=7,以x为自变量,试写出关于x函数解析式,并求出定义域.
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由题意可得(2+x)y=7-x,即y=
.再根据
>0,x>0求得函数的定义域.
| 7-x |
| x+2 |
| 7-x |
| x+2 |
解答:
解:∵x、y均为正值,且满足x+2y+xy=7,
即 (2+x)y=7-x,即y=
.
以x为自变量,可得函数的解析式为 y=
.
再根据
>0,x>0求得 0<x<7,
∴关于x函数解析式为y=
,定义域为(0,7).
即 (2+x)y=7-x,即y=
| 7-x |
| x+2 |
以x为自变量,可得函数的解析式为 y=
| 7-x |
| x+2 |
再根据
| 7-x |
| x+2 |
∴关于x函数解析式为y=
| 7-x |
| x+2 |
点评:本题主要考查求函数的解析式和定义域,属于基础题.

练习册系列答案
相关题目
下列命题中,真命题是( )
| A、命题“若p,则q”的否命题是“若p,则¬q” | ||
B、a+b=0的充要条件是
| ||
| C、已知命题p、q,若“p∨q”为假命题,则命题p与q一真一假 | ||
| D、命题p:?x∈R,使得x2+1<0,则¬p:?x∈R,使得x2+1≥0 |
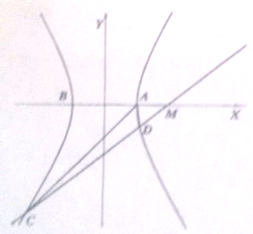 如图所示,已知双曲线
如图所示,已知双曲线