题目内容
甲船在A处观察乙船,乙船在它的北偏东60°的方向,两船相距a海里的B处,乙船正向北行驶,若甲船是乙船速度的
倍,甲船为了尽快追上乙船,则应取北偏东 (填角度)的方向前进.
| 3 |
考点:解三角形的实际应用
专题:应用题,解三角形
分析:根据题意画出图形,求出∠CAB与∠B的度数,设出追上乙船的时间,表示出BC与AC,在三角形ABC中,利用正弦定理列出关系式,即可求出θ的度数.
解答:
解:根据题意得:∠CAB=60°-θ,∠B=120°,设追上乙船的时间为x,则有BC=x,AC=
x,
在△ABC中,利用正弦定理
=
,即
=
,
∴
=
sin(60°-θ),即sin(60°-θ)=
,
∴60°-θ=30°,即θ=30°.
故答案为:30°
| 3 |
在△ABC中,利用正弦定理
| BC |
| sin∠CAB |
| AC |
| sinB |
| x |
| sin(60°-θ) |
| ||
| sin120° |
∴
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴60°-θ=30°,即θ=30°.
故答案为:30°
点评:此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若角α的终边在第二象限且经过点P(-1,
),则sinα等于( )
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都有f(x)<0成立,则实数m的取值范围是( )
| A、(0,1) | ||||
B、(0,
| ||||
| C、(-1,0) | ||||
D、(-
|
一条直线与两条异面直线中的一条相交,那么它与另一条直线之间的位置关系是( )
| A、异面 | B、相交或平行或异面 |
| C、相交 | D、平行 |
设f(x)=
,则f[f(ln2+1)]=( )
|
| A、log717 |
| B、2 |
| C、7 |
| D、log7(8e2+1) |
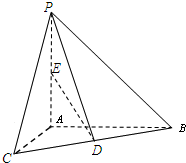 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D、E分别是BC、AP的中点.求异面直线AC与ED所成的角的大小为