题目内容
若f(x)是定义在(0,+∞)上的增函数,且f(
)=f(x)-f(y).
(1)求f(1)的值;
(2)解不等式:f(x-1)<0;
(3)若f(2)=1,解不等式f(2x+1)-f(23-2x)<2.
| x |
| y |
(1)求f(1)的值;
(2)解不等式:f(x-1)<0;
(3)若f(2)=1,解不等式f(2x+1)-f(23-2x)<2.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)问采用赋值法求出f(1)的值;
(2)根据函数的单调性将原不等式转化为一元一次不等式,解得即可
(3)问首先由f(2)=1分析出f(4)=2,再根据函数的单调性将原不等式转化为一元二次不等式.
(2)根据函数的单调性将原不等式转化为一元一次不等式,解得即可
(3)问首先由f(2)=1分析出f(4)=2,再根据函数的单调性将原不等式转化为一元二次不等式.
解答:
解:(1)令x=y=1,则有f(1)=f(1)-f(1)=0;
(2)∵f(x-1)<0=f(1),
又f(x)是定义在(0,+∞)上的增函数
∴x-1<1
解得0<x<2,
故不等式的解集为(0,2)
(3)令x=4,y=2,则有f(2)=f(4)-f(2);
∴f(4)=2f(2)=2,
∵f(2x+1)-f(23-2x)<2.
∴f(2x+1÷23-2x)<f(4).
∴f(23x-2)<f(4).
∵f(x)是定义在(0,+∞)上的增函数,
∴23x-2<22,
∴3x-2<2,
解得0<x<
故不等式的解集为:(0,
).
(2)∵f(x-1)<0=f(1),
又f(x)是定义在(0,+∞)上的增函数
∴x-1<1
解得0<x<2,
故不等式的解集为(0,2)
(3)令x=4,y=2,则有f(2)=f(4)-f(2);
∴f(4)=2f(2)=2,
∵f(2x+1)-f(23-2x)<2.
∴f(2x+1÷23-2x)<f(4).
∴f(23x-2)<f(4).
∵f(x)是定义在(0,+∞)上的增函数,
∴23x-2<22,
∴3x-2<2,
解得0<x<
| 4 |
| 3 |
故不等式的解集为:(0,
| 4 |
| 3 |
点评:本题考查抽象函数及其应用,考查赋值法,突出考查函数单调性的应用与解不等式组的能力,属于中档题

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
一条直线与两条异面直线中的一条相交,那么它与另一条直线之间的位置关系是( )
| A、异面 | B、相交或平行或异面 |
| C、相交 | D、平行 |
一个样本a,3,5,7的平均数是5,则这个样本的方差是( )
| A、2 | ||
B、
| ||
| C、4 | ||
| D、1 |
 某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是( )
某几何体正视图与侧视图相同,其正视图与俯视图如图所示,且图中的四边形都是边长为2的正方形,正视图中两条虚线互相垂直,则该几何体的体积是( )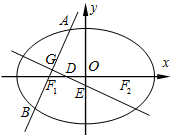 如图,已知椭圆C:
如图,已知椭圆C: