题目内容
12．在函数①y=2x； ②y=2-2x；③f（x）=x+x-1； ④f（x）=x-x-3中，存在零点且为奇函数的序号是④．分析 逐一分析给定中个函数的奇偶性及零点存在性，可得结论．
解答 解：函数①y=2x不存在零点且为非奇非偶函数，故不满足条件；
函数②y=2-2x存在零点1，但为非奇非偶函数，故不满足条件；
函数③f（x）=x+x-1不存在零点，为奇函数，故不满足条件；
函数④f（x）=x-x-3存在零点1且为奇函数，故满足条件；
故答案为：④．
点评 本题考查的知识点是函数的奇偶性，函数零点的存在性及个数判断，难度中档．
练习册系列答案
阅读快车系列答案
相关题目
2．设函数f（x）在R上存在导函数f′（x），对任意的实数x都有f（x）=2x2-f（-x），当x∈（-∞，0）时，f′（x）+1＜2x．若f（m+2）≤f（-m）+4m+4，则实数m的取值范围是（ ）
| A． | [-$\frac{1}{2}$，+∞） | B． | [-$\frac{3}{2}$，+∞） | C． | [-1，+∞） | D． | [-2，+∞） |
3．已知由不等式$\left\{{\begin{array}{l}{x≥y}\\{y≥0}\\{x+y-4≤0}\end{array}}\right.$所确定的平面区域为M，由不等式x2+y2≤8所确定的平面区域为N，区域M内随机抽取一个点，该点同时落在区域N内的概率是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{2}$ | C． | $\frac{π}{16}$ | D． | $\frac{π}{4}$ |
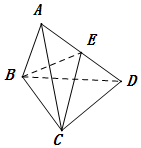如图所示，△ABC和△BCD都是正三角形，平面ABC⊥平面BCD，连接AD，E是线段AD的中点．
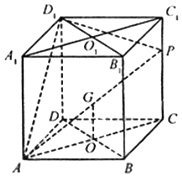如图，在棱长为1的正方体中，P是侧棱CC1上的一点，CP=m
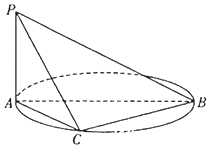如图，AB是圆O的直径，PA垂直圆所在的平面，C是圆上的点．