题目内容
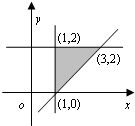已知点（x，y）在如图所示的平面区域（阴影部分）内运动，则z=x2+y2的最大值是（ ）| A、1 | B、3 | C、5 | D、13 |
考点：简单线性规划
专题：不等式的解法及应用
分析：根据z的几何意义，利用数形结合即可得到结论．
解答：
解：z的几何意义为区域内的点到原点的距离的平方，
由图象可知当点位于点（3，2）时，
z取得最大值，
则z=x2+y2=32+22=9+4=13，
故选：D．
由图象可知当点位于点（3，2）时，
z取得最大值，
则z=x2+y2=32+22=9+4=13，
故选：D．
点评：本题主要考查线性规划的应用，根据z的几何意义是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
曲线y=sinx，x∈[0，2π]与x轴围成的面积为（ ）
| A、4 | B、3 | C、2 | D、0 |
已知
，
是夹角为60°的两个单位向量，若
=
+
，
=-4
+2
，则
与
的夹角为（ ）
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
| A、30° | B、60° |
| C、120° | D、150° |
在吸烟与患肺病这两个分类变量的计算中，若从统计量计算中得出有99%的把握说吸烟与患肺病有关的结论，下列说法中正确的是（ ）
| A、若某人吸烟，那么他有99%的可能性患有肺病 |
| B、在100个吸烟者中必有99人患肺病 |
| C、在100个吸烟者中必有1个患肺病 |
| D、所得结论错误的可能性少于1% |
设i为虚数单位，则复数
为（ ）
| 3+4i |
| i3 |
| A、-4-3i | B、-4+3i |
| C、4+3i | D、4-3i |
过点P（2，
）作双曲线y=
的切线，则此切线的斜率等于（ ）
| 1 |
| 2 |
| 1 |
| x |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
下列命题为真命题的是（ ）
| A、?x∈R，sinx＞2 |
| B、?x∈R，x2≥0 |
| C、所有的等腰三角形都是等边三角形 |
| D、所有的平行向量都相等 |
袋中有大小相同的2个红球，4个白球，从袋中有放回地依次摸取2球，则两次均取出白球的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
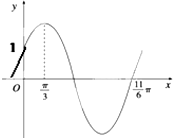已知函数f（x）=Asin（ωx+φ）（ω＞0，0＜φ＜