题目内容
在吸烟与患肺病这两个分类变量的计算中，若从统计量计算中得出有99%的把握说吸烟与患肺病有关的结论，下列说法中正确的是（ ）
| A、若某人吸烟，那么他有99%的可能性患有肺病 |
| B、在100个吸烟者中必有99人患肺病 |
| C、在100个吸烟者中必有1个患肺病 |
| D、所得结论错误的可能性少于1% |
考点：独立性检验的基本思想
专题：计算题,概率与统计
分析：有99%的把握认为吸烟与患肺病有关系，这一句话的意思是有有99%的把握认为这个推理是正确的，有1%的可能性认为推理出现错误，得到结果．
解答：
解：我们有99%的把握认为吸烟与患肺病有关系，这一句话的意思是有99%的把握认为这个推理是正确的，有1%的可能性认为推理出现错误，
故选：D．
故选：D．
点评：本题是一个独立性检验，我们可以利用临界值的大小来决定是否拒绝原来的统计假设，若值较大就拒绝假设，即认为两个事件有关．
练习册系列答案
相关题目
△ABC中，a=x，b=2，∠B=45°，则“2＜x＜2
”是“△ABC有两个解”的（ ）
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
已知平面内两定点A（-5，0），B（5，0），动点M满足|MA|-|MB|=10，则点M的轨迹是（ ）
| A、两条射线 | B、双曲线 |
| C、一条射线 | D、双曲线的一支 |
已知角α的终边与单位圆相交于点P（sin
，cos
），则sinα=（ ）
| 11π |
| 6 |
| 11π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知x＞0，y＞0，且2x+y=1，则
+
的最小值是（ ）
| 1 |
| x |
| 2 |
| y |
| A、8 | B、6 | C、3 | D、2 |
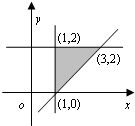已知点（x，y）在如图所示的平面区域（阴影部分）内运动，则z=x2+y2的最大值是（ ）| A、1 | B、3 | C、5 | D、13 |
设f（x）=2x，则f（x）的一个原函数是（ ）
| A、x3 | ||
| B、x2-1 | ||
C、
| ||
| D、2x+c |
若α，β为锐角，cos（α+β）=
，cos（2α+β）=
，则cosα的值为（ ）
| 12 |
| 13 |
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |