题目内容
下列命题为真命题的是（ ）
| A、?x∈R，sinx＞2 |
| B、?x∈R，x2≥0 |
| C、所有的等腰三角形都是等边三角形 |
| D、所有的平行向量都相等 |
考点：命题的真假判断与应用
专题：简易逻辑
分析：利用全称命题与特称命题的概念判断各命题的真假即可得答案．
解答：
解：A，∵|sinx|≤1，∴不?x∈R，sinx＞2，即A错误；
B，?x∈R，x2≥0，正确；
C，所有的等腰三角形都是等边三角形，错误；
D，所有的平行向量都相等，错误，
∴命题为真命题的是B，
故选：B．
B，?x∈R，x2≥0，正确；
C，所有的等腰三角形都是等边三角形，错误；
D，所有的平行向量都相等，错误，
∴命题为真命题的是B，
故选：B．
点评：本题考查命题的真假判断与应用，着重考查全称命题与特称命题的概念及应用，属于基础题．
练习册系列答案
相关题目
y=cosx，x∈[0，2π]的图象与直线y=
的交点的个数为（ ）
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
已知角α的终边与单位圆相交于点P（sin
，cos
），则sinα=（ ）
| 11π |
| 6 |
| 11π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
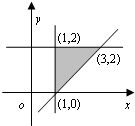已知点（x，y）在如图所示的平面区域（阴影部分）内运动，则z=x2+y2的最大值是（ ）| A、1 | B、3 | C、5 | D、13 |
m、n是两条不同的直线，α、β、γ是三个不同的平面，则下列命题正确的是（ ）
| A、若α⊥β，α⊥γ，则β⊥γ |
| B、若m、n与α所成的角相等，则m∥n |
| C、若m⊥α，m∥β，则α⊥β |
| D、若m∥n，m?α，则n∥α |
设f（x）=2x，则f（x）的一个原函数是（ ）
| A、x3 | ||
| B、x2-1 | ||
C、
| ||
| D、2x+c |
sinα=
，0＜α＜π，sin2α=（ ）
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
已知数列{an}为等差数列，且a3+a9=20，则S11=（ ）
| A、110 | B、220 |
| C、200 | D、55 |