题目内容
曲线y=sinx，x∈[0，2π]与x轴围成的面积为（ ）
| A、4 | B、3 | C、2 | D、0 |
考点：正弦函数的图象
专题：计算题
分析：根据对称性，确定被积函数与被积区间，用定积分表示面积，即可求得结论．
解答：
解：由题意，根据对称性可得x轴与曲线y=sinx在x∈[0，2π]内所围成的封闭图形的面积为
2
sinxdx=2（-cosx）
=-2cosπ+2cos0=4，
故答案为：4
2
| ∫ | π 0 |
| | | π 0 |
故答案为：4
点评：本题考查利用定积分求不规则图形的面积，解题的关键是确定被积函数与被积区间，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
中心在原点，实轴长为10，虚轴长为6的双曲线的标准方程为（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
圆台母线与底面成45°角，侧面积为3
π，则它的轴截面面积是（ ）
| 2 |
| A、2 | ||
| B、3 | ||
C、
| ||
D、3
|
y=cosx，x∈[0，2π]的图象与直线y=
的交点的个数为（ ）
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
△ABC中，a=x，b=2，∠B=45°，则“2＜x＜2
”是“△ABC有两个解”的（ ）
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
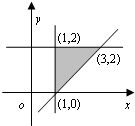已知点（x，y）在如图所示的平面区域（阴影部分）内运动，则z=x2+y2的最大值是（ ）| A、1 | B、3 | C、5 | D、13 |