题目内容
袋中有大小相同的2个红球，4个白球，从袋中有放回地依次摸取2球，则两次均取出白球的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：古典概型及其概率计算公式
专题：概率与统计
分析：第一次和第二次取到红球的概率都是
，由此能求出连续取两次都是红球的概率．
| 2 |
| 3 |
解答：
解：连续取两次都是红球的概率是
×
=
故选：C
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
故选：C
点评：本题主要考查了等可能事件的概率，以及对立事件和古典概型的概率等有关知识，是历年高考的必考题型．解题时要认真审题，注意排列组合和概率知识的灵活运用．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
△ABC中，a=x，b=2，∠B=45°，则“2＜x＜2
”是“△ABC有两个解”的（ ）
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
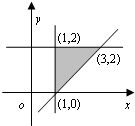已知点（x，y）在如图所示的平面区域（阴影部分）内运动，则z=x2+y2的最大值是（ ）| A、1 | B、3 | C、5 | D、13 |
设f（x）=2x，则f（x）的一个原函数是（ ）
| A、x3 | ||
| B、x2-1 | ||
C、
| ||
| D、2x+c |
sinα=
，0＜α＜π，sin2α=（ ）
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、±
| ||
D、
|
下列说法错误的是（ ）
| A、一个平面内有两条直线与另外一个平面平行，则这两个平面平行 |
| B、一个平面内任何直线都与另外一个平面平行，则这两个平面平行 |
| C、一个平面内两条相交直线与另外一个平面平行，则这两个平面平行 |
| D、垂直于同一个平面的两条直线平行 |
已知数列{an}为等差数列，且a3+a9=20，则S11=（ ）
| A、110 | B、220 |
| C、200 | D、55 |
若α，β为锐角，cos（α+β）=
，cos（2α+β）=
，则cosα的值为（ ）
| 12 |
| 13 |
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
在△ABC中，CA=3CB，cosC=-