题目内容
5.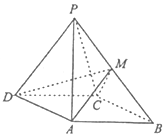 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为2$\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为2$\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.(Ⅰ)求证:PA⊥平面CDM
(Ⅱ)求二面角D-MC-A的余弦值.
分析 (I)取CD的中点O,连结PO,OA,则可证明PO⊥平面ABCD,OA⊥OC,以O为原点建立空间坐标系,利用向量证明PA⊥DC,PA⊥DM即可;
(II)求出平面ACM的法向量$\overrightarrow{n}$,求出cos<$\overrightarrow{n},\overrightarrow{PA}$>即可得出答案.
解答  解:(I)证明:取CD的中点O,连结PO,OA,
解:(I)证明:取CD的中点O,连结PO,OA,
∵△PDC是正三角形,∴PO⊥CD,
又平面PCD⊥平面ABCD,平面PCD∩平面ABCD=O,PO?平面PCD,
∴PO⊥平面ABCD,
∵底面ABCD是边长为2$\sqrt{3}$的菱形,∠DAB=120°,
∴△ACD是等边三角形,∴OA⊥CD,
以O为原点建立空间直角坐标系如图所示:
则A(3,0,0),P(0,0,3),D(0,-$\sqrt{3}$,0),B(3,2$\sqrt{3}$,0),C(0,$\sqrt{3}$,0),
∵M是PC的中点,∴M($\frac{3}{2}$,$\sqrt{3}$,$\frac{3}{2}$),
∴$\overrightarrow{PA}$=(3,0,-3),$\overrightarrow{DC}$=(0,2$\sqrt{3}$,0),$\overrightarrow{DM}$=($\frac{3}{2}$,2$\sqrt{3}$,$\frac{3}{2}$),
∴$\overrightarrow{PA}•\overrightarrow{DC}$=0,$\overrightarrow{PA}•\overrightarrow{DM}$=0,
∴PA⊥DC,PA⊥DM,
又DC∩DM=M,DC?平面DCM,DM?平面DCM,
∴PA⊥平面DCM.
(II)$\overrightarrow{CM}$=($\frac{3}{2}$,0,$\frac{3}{2}$),$\overrightarrow{CA}$=(3,-$\sqrt{3}$,0),
设平面CAM的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CM}=0}\\{\overrightarrow{n}•\overrightarrow{CA}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{\frac{3}{2}x+\frac{3}{2}z=0}\\{3x-\sqrt{3}y=0}\end{array}\right.$,令x=1得$\overrightarrow{n}$=(1,$\sqrt{3}$,-1),
又PA⊥平面DCM,∴$\overrightarrow{PA}$=(3,0,-3)是平面DCM的一个法向量,
∴cos<$\overrightarrow{PA},\overrightarrow{n}$>=$\frac{\overrightarrow{PA}•\overrightarrow{n}}{|\overrightarrow{PA}||\overrightarrow{n}|}$=$\frac{6}{\sqrt{5}•3\sqrt{2}}$=$\frac{\sqrt{10}}{5}$.
∴二面角D-MC-A的余弦值为$\frac{\sqrt{10}}{5}$.
点评 本题考查了线面垂直的判定,空间向量在立体几何的应用,属于中档题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
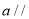 平面
平面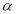 ,直线
,直线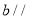 平面
平面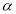 ,则直线
,则直线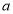 不一定平行于直线
不一定平行于直线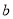
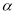 不垂直于平面
不垂直于平面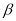 ,则
,则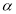 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面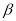
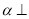 平面
平面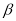 ,则
,则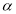 内一定不存在直线平行于平面
内一定不存在直线平行于平面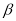
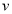 ,平面
,平面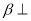 平面
平面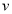 ,
,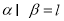 ,则
,则 一定垂直于平面
一定垂直于平面
 所得弦长为2,则圆心C的轨迹方程为( )
所得弦长为2,则圆心C的轨迹方程为( )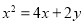 B.
B.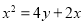
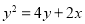 D.
D.