题目内容
设方程lnx=5-x的解为x0,则关于x的不等式x-1>x0的最小整数解为 .
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:由方程lnx=5-x的解为x0,我们易得函数y=lnx-5+x的零点为x0,根据函数零点的判定定理,我们可得x0∈(3,4),根据不等式的性质我们易求出等式x-2<x0的最大整数解.
解答:
解:由方程lnx=5-x的解为x0,我们易得函数f(x)=lnx-5+x的零点为x0,
由于函数f(x)=lnx-5+x在(0,+∞)上单调递增,f(3)<0,f(4)>0,
可得x0∈(3,4).
关于x的不等式x-1>x0,即关于x的不等式x>1+x0,
故关于x的不等式x-1>x0的最小整数解为5,
故答案为:5.
由于函数f(x)=lnx-5+x在(0,+∞)上单调递增,f(3)<0,f(4)>0,
可得x0∈(3,4).
关于x的不等式x-1>x0,即关于x的不等式x>1+x0,
故关于x的不等式x-1>x0的最小整数解为5,
故答案为:5.
点评:本题考查的知识点是函数零点的判断定理,及不等式的性质,其中根据零点存在定理,求出x0∈(2,3)是解答本题的关键,属于基础题.

练习册系列答案
相关题目
平面向量
,
满足|3
•
|≤4,则向量
•
的最小值为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
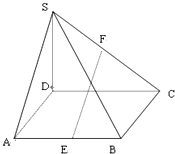 如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3.
如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E、F分别为AB、SC的中点,且AD=SD=2,DC=3. 如图在△ABC中,AB=2,AC=3,D为BC的中点,则向量
如图在△ABC中,AB=2,AC=3,D为BC的中点,则向量