题目内容
A={x|2≤x≤6}，B={x|3x-7≥8-2x}，
（1）A∪B，∁R（A∩B）
（2）若C={x|a-4＜x≤a+4}，且A⊆C，求a．
（1）A∪B，∁R（A∩B）
（2）若C={x|a-4＜x≤a+4}，且A⊆C，求a．
考点：子集与交集、并集运算的转换
专题：集合
分析：（1）由A与B，即可求出两集合的并集和交集；再由全集R及集合A与B的交集，求出A∩B的补集即可；
（2）根据A⊆C，由A与C求出a的范围即可．
（2）根据A⊆C，由A与C求出a的范围即可．
解答：
解：（1）A={x|2≤x≤6}，B={x|x≥3}，
∴A∩B={x|3≤x≤6}，
∴CR（A∪B）={x|x＜3或x＞6}；
（2）∵C={x|a-4＜x≤a+4}，且A⊆C，
∴
，
∴2≤a＜6
∴A∩B={x|3≤x≤6}，
∴CR（A∪B）={x|x＜3或x＞6}；
（2）∵C={x|a-4＜x≤a+4}，且A⊆C，
∴
|
∴2≤a＜6
点评：此题考查了并集、交集及其运算，熟练掌握并集、交集的定义是解本题的关键．
练习册系列答案
相关题目
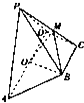如图四棱锥P-ABCD的底面是一等腰梯形，其中AD∥BC，其中AD=3BC=6，AB=DC=2