题目内容
12.在△ABC中,已知角A的正切值为函数y=lnx-$\frac{2}{x}$在x=1处切线的斜率,且a=$\sqrt{10}$,b=2,则sinB=$\frac{3}{5}$.分析 求出函数的导数,得到切线的斜率,求出A的正切函数值,然后转化利用正弦定理求解即可.
解答 解:函数y=lnx-$\frac{2}{x}$,可得y′=$\frac{1}{x}+\frac{2}{{x}^{2}}$,∴f′(1)=3,
∴tanA=3,可得sinA=$\sqrt{ta{n}^{2}A•co{s}^{2}A}=\sqrt{ta{n}^{2}A•\frac{1}{1+ta{n}^{2}a}}$=$\frac{3\sqrt{10}}{10}$,
由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}$,可得sinB=$\frac{bsinA}{a}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查函数的导数的应用,三角函数的应用,正弦定理,考查计算能力.

练习册系列答案
相关题目
2.2016年是红色长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神,首先在甲、乙、丙、丁四个不同的公园进行支持签名活动
然后在各公园签名的人中按分层抽样的方式抽取10名幸运之星回答问题,从10个关于长征的问题中随机抽取4个问题让幸运之星回答,全部答对的幸运之星获得一份纪念品.
(Ⅰ)求此活动轴个各公园幸运之星的人数
(Ⅱ)若乙公园中每位幸运之星对每个问题答对的概率均为$\frac{\sqrt{2}}{2}$,求恰好2位幸运之星获得纪念品的概率
(Ⅲ)若幸运之星小李对其中8个问题能答对,而另外2个问题答不对,记小李答对的问题数为X,求X的分布列及数学期望E(X)
| 公园 | 甲 | 乙 | 丙 | 丁 |
| 获得签名人数 | 45 | 60 | 30 | 15 |
(Ⅰ)求此活动轴个各公园幸运之星的人数
(Ⅱ)若乙公园中每位幸运之星对每个问题答对的概率均为$\frac{\sqrt{2}}{2}$,求恰好2位幸运之星获得纪念品的概率
(Ⅲ)若幸运之星小李对其中8个问题能答对,而另外2个问题答不对,记小李答对的问题数为X,求X的分布列及数学期望E(X)
3.如图,在网格中粗线显示的为某几何体的三视图(正方形网格的边长为1),则该几何体的体积为( )
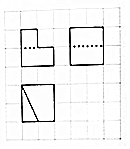

| A. | 5 | B. | 6 | C. | 6.5 | D. | 7 |
7.执行如图所救援程序框图,输出s的值为( )

| A. | 1 | B. | $\sqrt{2015}$-1 | C. | $\sqrt{2016}$-1 | D. | $\sqrt{2017}$-1 |
17.如图,O是坐标原点,M、N是单位圆上的两点,且分别在第一和第三象限,则$|\overrightarrow{OM}+\overrightarrow{ON}|$的范围为[0.$\sqrt{2}$).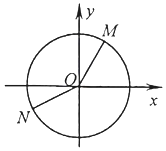

2.已知全集U=R,集合A={x|x<-$\frac{1}{2}$或x>1},B={x|-1≤x≤2,x∈Z},则图中阴影部分所表示的集合等于( )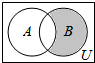

| A. | {-1,2} | B. | {-1,0} | C. | {0,1} | D. | {1,2} |