题目内容
20.定义在R上的函数y=f(x)为减函数,且函数y=f(x-1)的图象关于点(1,0)对称,若f(x2-2x)+f(2b-b2)≤0,且0≤x≤2,则x-b的取值范围是( )| A. | [-2,0] | B. | [-2,2] | C. | [0,2] | D. | [0,4] |
分析 设P(x,y)为函数y=f(x-1)的图象上的任意一点,关于(1,0)对称点为(2-x,-y),可得f(2-x-1)=-f(x-1),即f(1-x)=-f(x-1).由于不等式f(x2-2x)+f(2b-b2)≤0化为f(x2-2x)≤-f(2b-b2)=f(1-1-2b+b2)=f(b2-2b),再利用函数y=f(x)为定义在R上的减函数,可得x2-2x≥b2-2b,可画出可行域,进而得出答案.
解答  解:设P(x,y)为函数y=f(x-1)的图象上的任意一点,关于(1,0)对称点为(2-x,-y),
解:设P(x,y)为函数y=f(x-1)的图象上的任意一点,关于(1,0)对称点为(2-x,-y),
∴f(2-x-1)=-f(x-1),即f(1-x)=-f(x-1).
∴不等式f(x2-2x)+f(2b-b2)≤0化为f(x2-2x)≤-f(2b-b2)=f(1-1-2b+b2)
=f(b2-2b),
∵函数y=f(x)为定义在R上的减函数,
∴x2-2x≥b2-2b,
化为(x-1)2≥(b-1)2,
∵0≤x≤2,∴$\left\{\begin{array}{l}{0≤x≤1}\\{x≤b≤2-x}\end{array}\right.$或$\left\{\begin{array}{l}{1≤x≤2}\\{2-x≤b≤x}\end{array}\right.$.
画出可行域.设x-b=z,则b=x-z,由图可知:当直线b=x-z经过点(0,2)时,z取得最小值-2.
当直线b=x-z经过点(2,0)时,z取得最大值2.
综上可得:x-b的取值范围是[-2,2].
故选B.
点评 本题综合考查了函数的对称性、单调性、线性规划的可行域及其最值、直线的平移等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.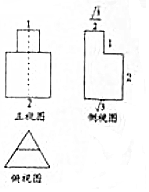 已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )
已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )
 已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )
已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{9\sqrt{3}}}{4}$ | C. | $3\sqrt{3}$ | D. | $\frac{{9\sqrt{3}}}{2}$ |
5.学校某文具商店经营某种文具,商店每销售一件该文具可获利3元,若供大于求则削价处理,每处理一件文具亏损1元;若供不应求,则可以从外部调剂供应,此时每件文具仅获利2元.为了了解市场需求的情况,经销商统计了去年一年(52周)的销售情况.
以去年每周的销售量的频率为今年每周市场需求量的概率.
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?
| 销售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?
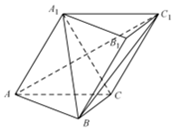 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.