题目内容
在直角梯形ABCD中，∠A=90°，∠B=30°，AB=2
，BC=2，点E在线段CD上，若
=
+μ
，则μ的取值范围是（ ）
| 3 |
| AE |
| AD |
| AB |
| A、[0，1] | ||
B、[0，
| ||
C、[0，
| ||
D、[
|
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，过点C作CF⊥AB，垂足为F．在Rt△BCF中，∠B=30°．可得CF=1，BF=
．再利用已知AB=2
，可得AF=
．由四边形AFCD是平行四边形，可得CD=AF=
=
AB．再利用向量的三角形法则和向量共线定理即可得出．
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
解答：
解：如图所示，
过点C作CF⊥AB，垂足为F．
在Rt△BCF中，∠B=30°．
∴CF=1，BF=
．
∵AB=2
，∴AF=
．
由四边形AFCD是平行四边形，可得CD=AF=
=
AB．
∵
=
+
=
+μ
，
∴
=μ
，∵
∥
，
=
，
∴0≤μ≤
．
故选：C．
过点C作CF⊥AB，垂足为F．
在Rt△BCF中，∠B=30°．
∴CF=1，BF=
| 3 |
∵AB=2
| 3 |
| 3 |
由四边形AFCD是平行四边形，可得CD=AF=
| 3 |
| 1 |
| 2 |
∵
| AE |
| AD |
| DE |
| AD |
| AB |
∴
| DE |
| AB |
| DE |
| DC |
| DC |
| 1 |
| 2 |
| AB |
∴0≤μ≤
| 1 |
| 2 |
故选：C．
点评：本题考查了梯形的性质、含30°角的直角三角形的性质、向量的三角形法则和向量共线定理等基础知识与基本技能方法，属于中档题．
练习册系列答案
相关题目
如图，已知椭圆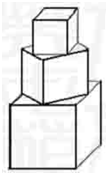
有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边中点，已知最底层正方体的棱长为2，且该塔形的表面积（含C最底层正方体的底面面积）超过39，则该塔形中正方体的个数至少是已知a＞0，x，y满足约束条件
，若z=2x+y的最小值为
，则a=（ ）
|
| 3 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知三角形ABC中，
•
＜0，则三角形ABC的形状为（ ）
| BA |
| BC |
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰直角三角形 |