题目内容
若向量
=(2,-1),
=(k,1),若
∥
,则实数k的值为 .
| a |
| b |
| a |
| b |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:利用向量共线定理即可得出.
解答:
解:∵
∥
,∴-1×k-1×2=0,解得k=-2.
故答案为:-2.
| a |
| b |
故答案为:-2.
点评:本题考查了向量共线定理,属于基础题.

练习册系列答案
相关题目
在直角梯形ABCD中,∠A=90°,∠B=30°,AB=2
,BC=2,点E在线段CD上,若
=
+μ
,则μ的取值范围是( )
| 3 |
| AE |
| AD |
| AB |
| A、[0,1] | ||
B、[0,
| ||
C、[0,
| ||
D、[
|
圆x2+(y-3)2=1上的动点P到点Q(2,3)的距离的最小值为( )
| A、2 | B、1 | C、3 | D、4 |
已知直线x+y+m=0与圆x2+y2=4交于不同的两点A,B,O是坐标原点,
+
|≥|
|,则实数m的取值范围是( )
| |OA |
| OB |
| AB |
| A、[-2,2] | ||||
B、[2,2
| ||||
C、(-2
| ||||
D、[2,2
|
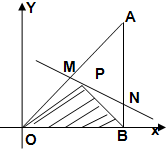 如图所示,将一块直角三角形板ABO置于平面直角坐标系中,已知AB=OB=1,AB⊥OB,点P
如图所示,将一块直角三角形板ABO置于平面直角坐标系中,已知AB=OB=1,AB⊥OB,点P