题目内容
求f(x)=6cos2x+6sinxcosx-4cos(x+
)•cos(
-x)的值域.
| π |
| 4 |
| π |
| 4 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:化简可得f(x)=sin(2x+φ)+3,其中tanφ=
,从而可求f(x)=6cos2x+6sinxcosx-4cos(x+
)•cos(
-x)的值域.
| 1 |
| 3 |
| π |
| 4 |
| π |
| 4 |
解答:
解:∵f(x)=6cos2x+6sinxcosx-4cos(x+
)•cos(
-x)
=3(1+cos2x)+3sin2x-2cos2x
=3sin2x+cos2x+3
=
sin(2x+φ)+3,其中tanφ=
∵-
≤sin(2x+φ)≤
∴f(x)=6cos2x+6sinxcosx-4cos(x+
)•cos(
-x)的值域为[3-
,3+
].
| π |
| 4 |
| π |
| 4 |
=3(1+cos2x)+3sin2x-2cos2x
=3sin2x+cos2x+3
=
| 10 |
| 1 |
| 3 |
∵-
| 10 |
| 10 |
∴f(x)=6cos2x+6sinxcosx-4cos(x+
| π |
| 4 |
| π |
| 4 |
| 10 |
| 10 |
点评:本题主要考察了三角函数中的恒等变换应用,属于基本知识的考查.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知S={1,2,3,…,21},A⊆S且A中有三个元素,若A中的元素可构成等差数列,则这样的集合A共有( )
| A、99个 | B、100个 |
| C、199个 | D、210个 |
设函数f(x)在x0点的某个邻域内有定义,则f(x)在x0处连续的充分必要条件是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、在x0的某个邻域内,f(x)=f(x0)+α(x),其中
|
若命题A的逆命题为B,命题A的否命题为C,则B是C的( )
| A、逆命题 | B、否命题 |
| C、逆否命题 | D、都不对 |
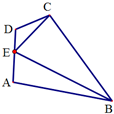 如图,在平面四边形ABCD中,DE=1.EC=
如图,在平面四边形ABCD中,DE=1.EC=