题目内容
11.下列各式中正确的个数是( )①(x7)′=7x6; ②(x-1)′=x-2; ③($\frac{1}{\sqrt{x}}$)′=-$\frac{1}{2}$x${\;}^{-\frac{3}{2}}$; ④($\root{5}{{x}^{2}}$)′=$\frac{2}{5}$x${\;}^{-\frac{3}{5}}$; ⑤(cosx)′=-sinx;
⑥(cos2)′=-sin2.
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据基本导数公式求导即可.
解答 解:①(x7)′=7x6; ②(x-1)′=-x-2; ③($\frac{1}{\sqrt{x}}$)′=-$\frac{1}{2}$x${\;}^{-\frac{3}{2}}$; ④($\root{5}{{x}^{2}}$)′=$\frac{2}{5}$x${\;}^{-\frac{3}{5}}$; ⑤(cosx)′=-sinx;⑥(cos2)′=0,
故正确的个数为4个,
故选:B
点评 本题考查了基本导数公式,属于基础题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
11.已知a,b,c∈(0,+∞),则下列三个数$a+\frac{4}{b}$,$b+\frac{9}{c}$,$c+\frac{16}{a}$( )
| A. | 都大于6 | B. | 至少有一个不大于6 | ||
| C. | 都小于6 | D. | 至少有一个不小于6 |
20.给出下面类比推理命题(其中R为实数集,C为复数集),正确的是( )
| A. | 若a,b∈R,则a-b>0⇒a>b,推出:若a,b∈C,则a-b>0⇒a>b | |
| B. | 若a,b∈R,则a2+b2=0⇒a=b=0,推出:若a,b∈C,则a2+b2=0⇒a=b=0 | |
| C. | 若a,b∈R,则a-b=0⇒a=b,推出:若a,b∈C,则a-b=0⇒a=b | |
| D. | 若x∈R,则|x|<1⇒-1<x<1,推出:若x∈C,则|x|<1⇒-1<x<1 |
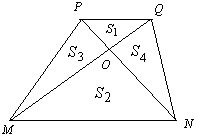 如图,在梯形PMNQ中,PQ∥MN,对角线PN和MQ相交于点O,并把梯形分成四部分,记这四部分的面积分别为S1,S2,S3,S4.试判断S1+S2和S3+S4的大小关系,并证明你的结论.
如图,在梯形PMNQ中,PQ∥MN,对角线PN和MQ相交于点O,并把梯形分成四部分,记这四部分的面积分别为S1,S2,S3,S4.试判断S1+S2和S3+S4的大小关系,并证明你的结论.