题目内容
9.设平面上的伸缩变换的坐标表达式为$\left\{\begin{array}{l}{x′=\frac{1}{2}x}\\{y′=3y}\end{array}\right.$,则在这一坐标变换下正弦曲线y=sinx的方程变为y=3sin2x.分析 根据伸缩变换的关系,利用代入法进行化简求解即可求得答案.
解答 解:由$\left\{\begin{array}{l}{x′=\frac{1}{2}x}\\{y′=3y}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2x′}\\{y=\frac{1}{3}y′}\end{array}\right.$,代入y=sinx得$\frac{1}{3}$y′=sin2x′,
即y′=3sin2x′,
则正弦曲线y=sinx的方程变换为y=3sin2x,
故答案为y=3sin2x.
点评 本题主要考查曲线和对称的变换,根据伸缩变换的关系,利用代入法是解决本题的关键,是基础题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
20.给出下面类比推理命题(其中R为实数集,C为复数集),正确的是( )
| A. | 若a,b∈R,则a-b>0⇒a>b,推出:若a,b∈C,则a-b>0⇒a>b | |
| B. | 若a,b∈R,则a2+b2=0⇒a=b=0,推出:若a,b∈C,则a2+b2=0⇒a=b=0 | |
| C. | 若a,b∈R,则a-b=0⇒a=b,推出:若a,b∈C,则a-b=0⇒a=b | |
| D. | 若x∈R,则|x|<1⇒-1<x<1,推出:若x∈C,则|x|<1⇒-1<x<1 |
17.设A={θ|θ为锐角},B={θ|θ为小于90°的角},C={θ|θ为第一象限的角},D={θ|θ为小于90°的正角},则下列等式中成立的是( )
| A. | A=B | B. | B=C | C. | A=C | D. | A=D |
19.已知复数z=$\frac{1+ai}{1-i}$(a∈R)的虚部为2,则a=( )
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |
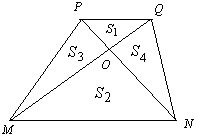 如图,在梯形PMNQ中,PQ∥MN,对角线PN和MQ相交于点O,并把梯形分成四部分,记这四部分的面积分别为S1,S2,S3,S4.试判断S1+S2和S3+S4的大小关系,并证明你的结论.
如图,在梯形PMNQ中,PQ∥MN,对角线PN和MQ相交于点O,并把梯形分成四部分,记这四部分的面积分别为S1,S2,S3,S4.试判断S1+S2和S3+S4的大小关系,并证明你的结论.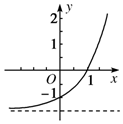 已知函数f(x)=ax+b(a>0,且a≠1).若f(x)的图象如图所示,
已知函数f(x)=ax+b(a>0,且a≠1).若f(x)的图象如图所示,