题目内容
含有三个实数的集合可表示为{a,
,1},也可表示为{a2,a+b,0}.求a+a2+a3+…+a2011+a2012的值.
| b |
| a |
考点:等比数列的前n项和,集合的相等
专题:等差数列与等比数列,集合
分析:根据集合相等和元素的互异性求出b和a的值,代入式子由等比数列的前n项和公式求值即可.
解答:
解:由题意得,{a,
,1}={a2,a+b,0},
所以
,即b=0,
则有{a,0,1}={a2,a,0},所以a2=1,
解得a=-1,
所以a+a2+a3+…+a2011+a2012=-1+1-1+…+(-1)+1
=
=0.
| b |
| a |
所以
|
则有{a,0,1}={a2,a,0},所以a2=1,
解得a=-1,
所以a+a2+a3+…+a2011+a2012=-1+1-1+…+(-1)+1
=
| (-1)[1-(-1)2012] |
| 1-(-1) |
点评:本题考查集合相等和元素的互异性,以及等比数列的前n项和公式的应用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
过点(π,1)且与曲线y=sinx+cosx在点(
,1)处的切线垂直的直线方程为( )
| π |
| 2 |
| A、y=x-1+π |
| B、y=x+1-π |
| C、y=-x+1+π |
| D、y=-x-1+π |
下列函数既是奇函数,又在区间[-1,1]上单调递减的是( )
| A、f(x)=sinx | ||
| B、f(x)=-|x+1| | ||
C、f(x)=
| ||
D、f(x)=ln
|
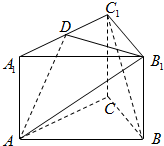 如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为
如图,正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为