Question

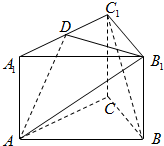如图，正三棱柱ABC-A₁B₁C₁的底面边长为a，侧棱长为

2

2

a，点D在棱A₁C₁上．
（1）若A₁D=DC₁，求证：直线BC₁∥平面AB₁D；
（2）是否存点D，使平面AB₁D⊥平面ABB₁A₁，若存在，请确定点D的位置，若不存在，请说明理由；
（3）请指出点D的位置，使二面角A₁-AB₁-D平面角的大小为arctan2．

Answer 1

考点：二面角的平面角及求法,平面与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（1）连结A₁B交AB₁于E点，由A₁D=DC₁，结合三角形中位线定理可得DE∥BC₁，然后根据线面平行的判定定理可得直线BC₁∥平面AB₁D．
（2）过点D作DN⊥AB₁于N，过点D作DM⊥A₁B₁于M，由线面垂直的判定定理及同一法，可得M，N应重合于B₁点，由于点D在棱A₁C₁上，故∠A₁B₁D≤∠A₁B₁C₁=60°，因此不存在这样的点使平面AB₁D⊥平面ABB₁A₁．
（3）连结MN，过A₁作A₁F⊥AB₁于F，由（2）的结论可得，∠MND为A₁-AB₁-D的平面角，设

A1D

A1C1

=λ，由二面角的正切值大小为2，构造关于λ的方程，从而指出D的位置．

解答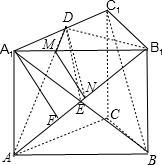： （1）证明：（1）连结A₁B交AB₁于E点，由A₁D=DC₁，结合三角形中位线定理可得DE∥BC₁，DE?面AB₁D 根据线面平行的判定定理可得直线BC₁∥平面AB₁D．
（2）假设存在D点，使平面AB₁D⊥平面ABB₁A₁，过D作DN⊥AB₁于N，则DN⊥面ABB₁A₁，过D作DM⊥面ABB₁A₁，E而过平面外一点有且只有一条直线与已知平面垂直，故M、N应重合于B₁点，则DB₁⊥A₁B₁，故∠A₁B₁D=90°
≤∠A₁B₁C₁=60°，显然矛盾，不存在这样的点．
（3）连结MN，过A₁点作A₁F⊥AB₁于F，由（2）得∠MND为二面角A₁-AB₁-D的平面角，故设

A1D

A1C1

=λ，则

A1M

A1B1

=

λ

2

，可得：DM=

3 aλ

2

，A1F=

3 a

3

，

MN

A1F

=1-

λ

2

，则MN=

3

3

a(1-

λ

2

)所以tanθ=

DM

MN

=-3+

6

2-λ

由于2=-3+

6

2-λ

解得：λ=

4

5

，即点D在A1C1上且

A1D

A1C1

=

4

5

时二面角A₁-AB₁-D平面角的大小为arctan2．

点评：本题考查的知识点：线面平行的判定定理，面面垂直的性质定理，反证法在实际问题中的应用，构造关于分点的方程及相关的运算问题．