题目内容
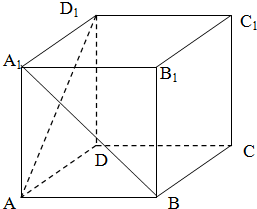 已知正方体ABCD-A1B1C1D1,求:
已知正方体ABCD-A1B1C1D1,求:(1)异面直线AD1与A1B所成的角;
(2)求AD1与平面ABCD所成的角;
(3)求二面角D1-AB-C的大小.
考点:二面角的平面角及求法,异面直线及其所成的角
专题:空间角
分析:(1)连结D1C,AC,则A1B∥D1C,从而异面直线AD1与A1B所成的角为∠AD1C,由△AD1C是等边三角形,能求出异面直线AD1与A1B所成的角的大小.
(2)因为DD1⊥平面ABCD,所以AD1与平面ABCD所成的角为∠D1AD,通过正方体的性质可求大小;
(3)因为D1A⊥AB,CB⊥AB,所以二面角D1-AB-C的平面角为∠D1AD=45°.
(2)因为DD1⊥平面ABCD,所以AD1与平面ABCD所成的角为∠D1AD,通过正方体的性质可求大小;
(3)因为D1A⊥AB,CB⊥AB,所以二面角D1-AB-C的平面角为∠D1AD=45°.
解答:
解:(1)连结D1C,AC,如图,

则△AD1C是等边三角形
∵A1B∥D1C,
∴异面直线AD1与A1B所成的角为∠AD1C,
∵△AD1C是等边三角形,
∴∠AD1C=60°,
∴异面直线AD1与A1B所成的角为60°.
(2)∵DD1⊥平面ABCD,∴AD1与平面ABCD所成的角为∠D1AD,
∵几何体是正方体,∴∠D1AD=45°;
(3)∵D1A⊥AB,CB⊥AB,BC∥AD,
∴二面角D1-AB-C的平面角为∠D1AD=45°.

则△AD1C是等边三角形
∵A1B∥D1C,
∴异面直线AD1与A1B所成的角为∠AD1C,
∵△AD1C是等边三角形,
∴∠AD1C=60°,
∴异面直线AD1与A1B所成的角为60°.
(2)∵DD1⊥平面ABCD,∴AD1与平面ABCD所成的角为∠D1AD,
∵几何体是正方体,∴∠D1AD=45°;
(3)∵D1A⊥AB,CB⊥AB,BC∥AD,
∴二面角D1-AB-C的平面角为∠D1AD=45°.
点评:本题考查了正方体中异面直线所成的角以及线面角和二面角;关键是将空间角转化为平面角来解答.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
已知直线y=-x+1与椭圆
+
=1(a>b>0)相交于A、B两点,若椭圆的离心率为
,焦距为2,则线段AB的长是( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
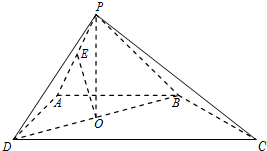 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.