题目内容
已知关于x的一次函数y=ax+b.
(Ⅰ)设集合A={-2,-1,1,2}和B={-2,2},分别从集合A和B中随机取一个数作为a,b,求函数y=ax+b是增函数的概率;
(Ⅱ)若实数a,b满足条件
,求函数y=ax+b的图象不经过第四象限的概率.
(Ⅰ)设集合A={-2,-1,1,2}和B={-2,2},分别从集合A和B中随机取一个数作为a,b,求函数y=ax+b是增函数的概率;
(Ⅱ)若实数a,b满足条件
|
考点:几何概型,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)根据古典概型的概率公式即可得到结论;
(Ⅱ)作出不等式组对应的平面区域,利用几何概型的概率公式即可得到结论.
(Ⅱ)作出不等式组对应的平面区域,利用几何概型的概率公式即可得到结论.
解答:
解:(Ⅰ)抽取全部结果所构成的基本事件空间为(-2,-2),(-2,2),(-1,-2),(-1,2),(1,-2),(1,2),(2,-2),(2,2),共8个.
设函数是增函数为事件A,∴a>0,有4个,
∴P(A)=
(Ⅱ)实数a,b满足条件
要函数y=ax+b的图象不经过第四象限
则需使a,b满足
,即
,对应的图形为正方形,面积为1,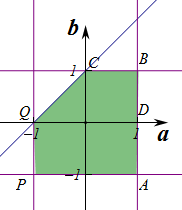
作出不等式组对应的平面区域如图:
则根据几何概型的概率公式可得函数y=ax+b的图象不经过第四象限的概率为
=
.
设函数是增函数为事件A,∴a>0,有4个,
∴P(A)=
| 1 |
| 2 |
(Ⅱ)实数a,b满足条件
|
则需使a,b满足
|
|

作出不等式组对应的平面区域如图:
则根据几何概型的概率公式可得函数y=ax+b的图象不经过第四象限的概率为
| 1 | ||
|
| 2 |
| 7 |
点评:本题主要考查古典概型和几何概型的概率的计算,要求熟练掌握相应的概率公式.

练习册系列答案
相关题目
在等比数列{an}中,Tn为前n项的积,若T3=1,
=2,则a13a14a15的值为( )
| T6 |
| T3 |
| A、16 | B、12 | C、8 | D、4 |
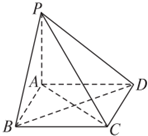 已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是
已知PA垂直于正方形ABCD所在平面,连接PB、PC、PD、AC、BD,则下列垂直关系中正确的序号是