题目内容
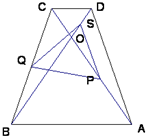 如图所示,等腰梯形ABCD中,AB∥CD,AD=CB,对角线AC与BD交于O,∠ACD=60°,点S、P、Q分别是OD、OA、BC的中点.
如图所示,等腰梯形ABCD中,AB∥CD,AD=CB,对角线AC与BD交于O,∠ACD=60°,点S、P、Q分别是OD、OA、BC的中点.(1)求证:△PQS是等边三角形;
(2)若AB=8,CD=6,求△PQS的面积;
(3)若△PQS与△AOD的面积比为4:5,求CD:AB的值.
考点:平行线分线段成比例定理
专题:选作题,立体几何
分析:(1)由于梯形ABCD是等腰梯形∠ACD=60°,可知△OCD与△OAB均为等边三角形.连接CS,BP根据等边三角形的性质可知△BCS与△BPC为直角三角形,再利用直角三角形的性质可知QS=BP=
BC,由中位线定理可知,QS=QP=PS=
BC,故△PQS是等边三角形;
(2)根据等腰梯形的性质及∠AOD=120°可求出等边三角形的边长,从而可得出答案.
(3)设CD=a,AB=b(a<b),根据题意表示出两面积的比,从而可得出答案.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据等腰梯形的性质及∠AOD=120°可求出等边三角形的边长,从而可得出答案.
(3)设CD=a,AB=b(a<b),根据题意表示出两面积的比,从而可得出答案.
解答:
(1)连接CS
∵ABCD是等腰梯形,且AC与BD相交于O,
∴AO=BO,CO=DO.
∵∠ACD=60°,∴△OCD与△OAB均为等边三角形.
∵S是OD的中点,∴CS⊥DO.
又SP是△OAD的中位线,∴SP=
AD=
BC.
∴SP=PQ=SQ.
故△SPQ为等边三角形.
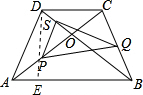
(2)作DE⊥AB,垂足为E,
∵AB=8,CD=6,
∴AE=1,BE=8-1=7,
∴DE=BE•tan60°=7
,
在Rt△ADE中,AD=2
,
∴PS=PQ=SQ=
,
∴S△PQS=
(3)设CD=a,AB=b(a<b),
BC2=SC2+BS2=a2+b2+ab,
∴S△SPQ=
(a2+ab+b2),
又△PQS与△AOD的面积比为4:5,S△AOD=S△BOC=
ab,
∴5×
(a2+ab+b2)=4×
ab,
即5a2-11ab+5b2=0,
故
=
∵ABCD是等腰梯形,且AC与BD相交于O,
∴AO=BO,CO=DO.
∵∠ACD=60°,∴△OCD与△OAB均为等边三角形.
∵S是OD的中点,∴CS⊥DO.
又SP是△OAD的中位线,∴SP=
| 1 |
| 2 |
| 1 |
| 2 |
∴SP=PQ=SQ.
故△SPQ为等边三角形.
(2)作DE⊥AB,垂足为E,
∵AB=8,CD=6,
∴AE=1,BE=8-1=7,
∴DE=BE•tan60°=7
| 3 |
在Rt△ADE中,AD=2
| 37 |
∴PS=PQ=SQ=
| 37 |

∴S△PQS=
37
| ||
| 4 |
(3)设CD=a,AB=b(a<b),
BC2=SC2+BS2=a2+b2+ab,
∴S△SPQ=
| ||
| 16 |
又△PQS与△AOD的面积比为4:5,S△AOD=S△BOC=
| ||
| 4 |
∴5×
| ||
| 16 |
| ||
| 4 |
即5a2-11ab+5b2=0,
故
| CD |
| AB |
11-
| ||
| 10 |
点评:本题主要考查等腰梯形及直角三角形的性质,三角形中位线定理.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
若a,b∈R,则下面四个式子中恒成立的是( )
| A、a2+3ab>2b2 | ||||
| B、a2+b2≥2(a-b-1) | ||||
| C、lg(1+a2)>0 | ||||
D、
|
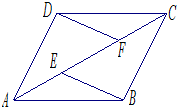 如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形.
如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形.