题目内容
若a，b∈R，则下面四个式子中恒成立的是（ ）
| A、a2+3ab＞2b2 | ||||
| B、a2+b2≥2（a-b-1） | ||||
| C、lg（1+a2）＞0 | ||||
D、
|
考点：不等式的基本性质
专题：不等式的解法及应用
分析：A．a=b=0时即可判断出；
B．a2+b2-2（a-b-1）=（a-1）2+（b+1）2≥0恒成立．
C．a=1时，lg（1+a2）=0，即可判断出；
D．取a＞b＞0即可判断出．
B．a2+b2-2（a-b-1）=（a-1）2+（b+1）2≥0恒成立．
C．a=1时，lg（1+a2）=0，即可判断出；
D．取a＞b＞0即可判断出．
解答：
解：A．a=b=0时不成立；
B．a2+b2-2（a-b-1）=（a-1）2+（b+1）2≥0恒成立．
C．a=0时，lg（1+a2）=0，因此不成立；
D．取a＞b＞0，可知不成立．
故选：B．
B．a2+b2-2（a-b-1）=（a-1）2+（b+1）2≥0恒成立．
C．a=0时，lg（1+a2）=0，因此不成立；
D．取a＞b＞0，可知不成立．
故选：B．
点评：本题考查了不等式的基本性质，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
，g（x）=-x2+4x-3，对于任意的a，存在b使方程f（a）=g（b）成立，则b的取值范围是（ ）
| 1 |
| ex+1 |
| A、（1，3） |
| B、（1，2）∪（2，3） |
| C、[1，3] |
| D、[1，2）∪（2，3] |
已知数列{an}共有2n+1项，其中奇数项通项公式为an=2n-1，则数列{an}的奇数项的和为（ ）
| A、2（2n+1-1）-n-1 | ||
B、
| ||
| C、2（4n+1-1）-n-1 | ||
D、
|
在直角坐标系xOy中，直线l的参数方程为
（t为参数）．曲线C的参数方程为
（θ为参数），则直线l和曲线C的公共点有（ ）
|
|
| A、0个 | B、1个 | C、2个 | D、无数个 |
集合{a，b，c，d}的子集有（ ）
| A、4个 | B、8个 |
| C、16个 | D、32个 |
已知函数f（x）=x-1+
（x＞-1）．当x=a时，f（x）取得最小值，则a=（ ）
| 9 |
| x+1 |
| A、2 | B、1 | C、-3 | D、-4 |
若某程序框图如图所示，当输入50时，则该程序运算后输出的结果是（ ）
| A、8 | B、6 | C、4 | D、2 |
已知函数f（x）=
（x∈R）时，则下列结论不正确的是（ ）
| x |
| 1+|x| |
| A、任意x∈R，等式f（-x）+f（x）=0恒成立 |
| B、存在m∈（0，1），使得方程|f（x）|=m有两个不等实数根 |
| C、对任意x1，x2∈R，若x1≠x2，则一定有f（x1）≠f（x2） |
| D、存在k∈（1，+∞），使得函数g（x）=f（x）-kx在R上有三个零点 |
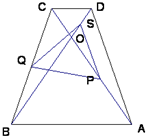如图所示，等腰梯形ABCD中，AB∥CD，AD=CB，对角线AC与BD交于O，∠ACD=60°，点S、P、Q分别是OD、OA、BC的中点．