题目内容
已知函数f(x)=x2+(lga+2)x+lgb满足f(-1)=-2,且对于任意x∈R,恒有f(x)≥2x成立.
(1)求实数a,b的值;
(2)y=
的定义域为R,求k的取值范围.
(1)求实数a,b的值;
(2)y=
| f(x)+(2k-4)x+k-1 |
考点:利用导数求闭区间上函数的最值
专题:函数的性质及应用
分析:(1)根据f(-1)=-2列一个关于a,b的方程,再根据f(x)≥2x恒成立,利用二次函数的性质列出另一个方程(不等式成立时只能取等号),联立解方程组即可;
(2)由题意,根号下的式子≥0在实数集上恒成立,经化简可知为二次函数函数值大于或等于0在R上恒成立,借助判别式容易解决.
(2)由题意,根号下的式子≥0在实数集上恒成立,经化简可知为二次函数函数值大于或等于0在R上恒成立,借助判别式容易解决.
解答:
解:(1)由f(-1)=-2,知lgb-lga+1=0,∴
=10.
又f(x)≥2x恒成立,所以x2+x•lga+lgb≥0恒成立,
故△=(lga)2-4lgb≤0.将
=10代入得:
(lgb)2-2lgb+1≤0,即(lgb-1)2≤0,即lgb=1.
故b=10,所以a=100.
(2)由(1)知f(x)=x2+4x+1,代入y=
化简后得:
y=
,因为该函数定义域为R,
所以x2+2kx+k≥0,x∈R恒成立,
根据二次函数的图象可知只需△=(2k)2-4k≤0即可,
解得0≤k≤1.
故k的取值范围是[0,1].
| a |
| b |
又f(x)≥2x恒成立,所以x2+x•lga+lgb≥0恒成立,
故△=(lga)2-4lgb≤0.将
| a |
| b |
(lgb)2-2lgb+1≤0,即(lgb-1)2≤0,即lgb=1.
故b=10,所以a=100.
(2)由(1)知f(x)=x2+4x+1,代入y=
| f(x)+(2k-4)x+k-1 |
y=
| x2+2kx+k |
所以x2+2kx+k≥0,x∈R恒成立,
根据二次函数的图象可知只需△=(2k)2-4k≤0即可,
解得0≤k≤1.
故k的取值范围是[0,1].
点评:本题考查了不等式的恒成立问题,此类问题一般是转化为函数的最值问题来解,而研究函数的最值往往要利用导数研究单调性,这是一种常规思路;当然作为二次不等式在R上的恒成立,利用二次函数的性质结合图象、判别式等似乎更简单.

练习册系列答案
相关题目
已知函数f(x)=x-1+
(x>-1).当x=a时,f(x)取得最小值,则a=( )
| 9 |
| x+1 |
| A、2 | B、1 | C、-3 | D、-4 |
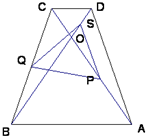 如图所示,等腰梯形ABCD中,AB∥CD,AD=CB,对角线AC与BD交于O,∠ACD=60°,点S、P、Q分别是OD、OA、BC的中点.
如图所示,等腰梯形ABCD中,AB∥CD,AD=CB,对角线AC与BD交于O,∠ACD=60°,点S、P、Q分别是OD、OA、BC的中点. 如图,在正方体OPRS-ABCD中,底面ABCD边长为2,M为OA的中点.
如图,在正方体OPRS-ABCD中,底面ABCD边长为2,M为OA的中点.