题目内容
椭圆的中心为原点O,一焦点为F(3,0),过焦点F引垂直于长轴的弦MN,已知从中心O看弦MN的视角等于从长轴端点看短轴的视角,求此椭圆的离心率和椭圆方程.
考点:椭圆的应用
专题:圆锥曲线的定义、性质与方程
分析:根据题意画出几何图形,从中心O看弦MN的视角等于从长轴端点看短轴的视角可得:∠MON=∠BAC,由椭圆的对称性可知:∠MOF=∠OAC,从而解得b=c=3,进而解得a=3
,从而解得答案.
| 2 |
解答:
解:设椭圆的方程为:
+
=1,由于c=5,如图: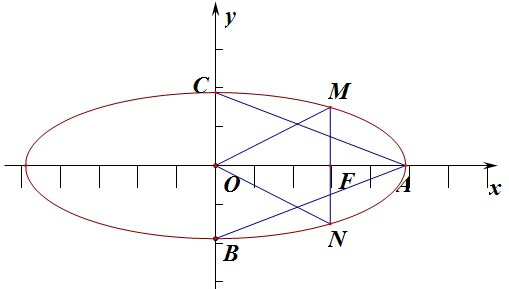
由题意可知:∠MON=∠BAC,
由椭圆的对称性可知:∠MOF=∠OAC,
∵MN⊥OA,F(3,0),
∴M(3,
),
∴tan∠MOF=
=
=
又tan∠OAC=
=
,
∴
=
,a=
=3
,
∴e=
=
=
,
椭圆的方程是:
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |

由题意可知:∠MON=∠BAC,
由椭圆的对称性可知:∠MOF=∠OAC,
∵MN⊥OA,F(3,0),
∴M(3,
| b2 |
| a |
∴tan∠MOF=
| MF |
| OF |
| ||
| c |
| b2 |
| ac |
又tan∠OAC=
| OC |
| OA |
| b |
| a |
∴
| b2 |
| ac |
| b |
| a |
| b2+c2 |
| 2 |
∴e=
| c |
| a |
| 3 | ||
3
|
| ||
| 2 |
椭圆的方程是:
| x2 |
| 18 |
| y2 |
| 9 |
点评:本题主要考查椭圆的几何性质和椭圆的标准方程,重点是利用好几何图形,属于中档题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
已知数列{an}共有2n+1项,其中奇数项通项公式为an=2n-1,则数列{an}的奇数项的和为( )
| A、2(2n+1-1)-n-1 | ||
B、
| ||
| C、2(4n+1-1)-n-1 | ||
D、
|
若某程序框图如图所示,当输入50时,则该程序运算后输出的结果是( )


| A、8 | B、6 | C、4 | D、2 |
已知函数f(x)=
(x∈R)时,则下列结论不正确的是( )
| x |
| 1+|x| |
| A、任意x∈R,等式f(-x)+f(x)=0恒成立 |
| B、存在m∈(0,1),使得方程|f(x)|=m有两个不等实数根 |
| C、对任意x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2) |
| D、存在k∈(1,+∞),使得函数g(x)=f(x)-kx在R上有三个零点 |
若a>b,则下列不等式中恒成立的是( )
A、
| ||||
B、
| ||||
| C、a2>b2 | ||||
| D、a3>b3 |
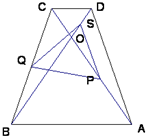 如图所示,等腰梯形ABCD中,AB∥CD,AD=CB,对角线AC与BD交于O,∠ACD=60°,点S、P、Q分别是OD、OA、BC的中点.
如图所示,等腰梯形ABCD中,AB∥CD,AD=CB,对角线AC与BD交于O,∠ACD=60°,点S、P、Q分别是OD、OA、BC的中点.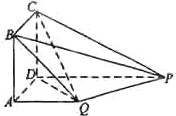 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=