题目内容
15.已知点A(1,0),直线l:x=-1,两个动圆均过点A且与l相切,其圆心分别为C1、C2,若动点M满足$2\overrightarrow{{C_2}M}=\overrightarrow{{C_2}{C_1}}+\overrightarrow{{C_2}A}$,则M的轨迹方程为y2=2x-1.分析 由抛物线的定义可得动圆的圆心轨迹方程为y2=4x,利用$2\overrightarrow{{C_2}M}=\overrightarrow{{C_2}{C_1}}+\overrightarrow{{C_2}A}$,确定坐标之间的关系,即可求出M的轨迹方程.
解答 解:由抛物线的定义可得动圆的圆心轨迹方程为y2=4x,
设C1(a,b),C2(m,n),M(x,y),则
∵动点M满足$2\overrightarrow{{C_2}M}=\overrightarrow{{C_2}{C_1}}+\overrightarrow{{C_2}A}$,
∴2(x-m,y-n)=(a-m,b-n)+(1-m,2-n),
∴2x=a+1,2y=b+2,
∴a=2x-1,b=2y-2,
∵b2=4a,
∴(2y-2)2=4(2x-1),即(y-1)2=2x-1.
故答案为:y2=2x-1.
点评 本题考查轨迹方程,考查向量知识的运用,考查学生分析解决问题的能力,确定坐标之间的关系是关键.

练习册系列答案
相关题目
7.已知$U=\{y|y={2^x},x≥-1\},A=\{x|\frac{1}{x-1}≥1\}$,则∁UA=( )
| A. | $[\frac{1}{2},2]$ | B. | [2,+∞) | C. | $[\frac{1}{2},1]∪(2,+∞)$ | D. | $[\frac{1}{2},2)∪(2,+∞)$ |
4.王先生购买了一部手机,欲使用中国移动“神州行”卡或加入联通的130网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
若王先生每月拨打本地电话的时间是拨打长途电话时间的5倍,若要用联通130应最少打多长时间的长途电话才合算.( )
| 网络 | 月租费 | 本地话费 | 长途话费 |
| 甲:联通130 | 12元 | 0.36元/分 | 0.06元/秒 |
| 乙:移动“神州行” | 无 | 0.60元/分 | 0.07元/秒 |
| A. | 300秒 | B. | 400秒 | C. | 500秒 | D. | 600秒 |
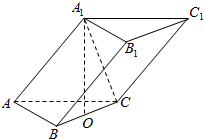 如图,在三棱柱ABC-A1B1C1中,已知A1在底面ABC内的射影是线段BC的中点,且A1O=OC,BC⊥AA1.
如图,在三棱柱ABC-A1B1C1中,已知A1在底面ABC内的射影是线段BC的中点,且A1O=OC,BC⊥AA1.