题目内容
4．王先生购买了一部手机，欲使用中国移动“神州行”卡或加入联通的130网，经调查其收费标准见下表：（注：本地电话费以分为计费单位，长途话费以秒为计费单位．）| 网络 | 月租费 | 本地话费 | 长途话费 |
| 甲：联通130 | 12元 | 0.36元/分 | 0.06元/秒 |
| 乙：移动“神州行” | 无 | 0.60元/分 | 0.07元/秒 |
| A． | 300秒 | B． | 400秒 | C． | 500秒 | D． | 600秒 |
分析 根据每月的通话时间和甲方式的收费标准，可知所需花费=月租费+本地话费+长途话费，可求所需话费y（元）与通话时间x（分钟）的函数关系式；将乙方式所需话费y（元）与通话时间x（分钟）的函数关系式求出，将两个式子进行比较，可得出较为省钱的入网方式．
解答 解：每月接打本地电话的时间是接打长途电话的5倍，王先生每月拨打长途电话时间为x（分钟），他所需话费y（元），联通130他所需话费y（元）与通话时间x（分钟）的函数关系式为y=12+0.36×5x+3.6x（x＞0）；
移动“神州行”他所需话费y（元）与通话时间x（分钟）的函数关系式为：y=0.6×5x+4.2x，
若要用联通130应最少打多长时间的长途电话才合算，可得：12+0.36×5x+3.6x＜0.6×5x+4.2x，
解得：x＞$\frac{20}{3}$（分钟）=400秒．
故选：B．
点评 本题主要是应用数学模型来解决实际问题，考查一次函数的应用．
练习册系列答案
名师导航单元期末冲刺100分系列答案
相关题目
12．已知点A（1，1），B（2，1），C（1，2），若-1≤λ≤2，2≤μ≤3，则$|{λ\overrightarrow{AB}+μ\overrightarrow{AC}}|$的取值范围是（ ）
| A． | [1，10] | B． | $[{\sqrt{5}，\sqrt{13}}]$ | C． | [1，5] | D． | $[{2，\sqrt{13}}]$ |
如图，已知双曲线C的右焦点为F，过它的右顶点A作实轴的垂线，与其一条渐近线相交于点B；若双曲线C的焦距为4，△OFB为等边三角形（O为坐标原点，即双曲线C的中心），则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$．
16．
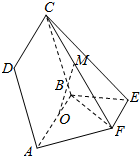如图所示，点E，F在以AB为直径的圆O（O为圆心）上，AB∥EF，平面ABCD⊥平面ABEF，且AB=2，AD=EF=1
（Ⅰ）设FC的中点为M，求证：OM∥面DAF；
（Ⅱ）求证：AF⊥面CBF．
如图所示，点E，F在以AB为直径的圆O（O为圆心）上，AB∥EF，平面ABCD⊥平面ABEF，且AB=2，AD=EF=1（Ⅰ）设FC的中点为M，求证：OM∥面DAF；
（Ⅱ）求证：AF⊥面CBF．
13．设x取实数，则f（x）与g（x）表示同一个函数的是（ ）
| A． | $f（x）={x^2}，g（x）=\sqrt{x^2}$ | B． | $f（x）=\frac{{{{（\sqrt{x}）}^2}}}{x}，g（x）=\frac{x}{{{{（\sqrt{x}）}^2}}}$ | ||
| C． | f（x）=1，g（x）=（x-1）0 | D． | $f（x）=\frac{{{x^2}-9}}{x+3}，g（x）=x-3$ |