题目内容
5.已知函数f(x)=lnx 图象与函数$g(x)=2\sqrt{x}$图象在交点处切线方程相同,则m的值为e.分析 先设出切点的坐标,求出f(x),g(x)的导数,得到关于m的方程组,求出m的值即可.
解答 解:设切点为P(x0,y0),
由$f(x)'=\frac{m}{x},g(x)'=\frac{1}{{\sqrt{x}}}$
则有题意得$\left\{\begin{array}{l}mln{x_0}=2\sqrt{x_0}\\ \frac{m}{x_0}=\frac{1}{{\sqrt{x_0}}}\end{array}\right.$,
解得m=e,
故答案为:e.
点评 本题考察了导数的应用,考察切线方程问题,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.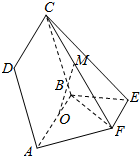 如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
(Ⅰ)设FC的中点为M,求证:OM∥面DAF;
(Ⅱ)求证:AF⊥面CBF.
 如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1(Ⅰ)设FC的中点为M,求证:OM∥面DAF;
(Ⅱ)求证:AF⊥面CBF.
13.设x取实数,则f(x)与g(x)表示同一个函数的是( )
| A. | $f(x)={x^2},g(x)=\sqrt{x^2}$ | B. | $f(x)=\frac{{{{(\sqrt{x})}^2}}}{x},g(x)=\frac{x}{{{{(\sqrt{x})}^2}}}$ | ||
| C. | f(x)=1,g(x)=(x-1)0 | D. | $f(x)=\frac{{{x^2}-9}}{x+3},g(x)=x-3$ |
15.设集合A={x|x2-x-2=0},B={-2,0,2},则A∩B=( )
| A. | ϕ | B. | {2} | C. | {0} | D. | {-2} |
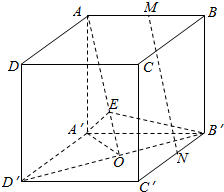 如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点.
如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点.