题目内容
已知函数f(x)=log2(
-5x)+3,则f(lna)+f(ln
)的值( )
| 1+25x2 |
| 1 |
| a |
| A、为-6 | B、为6 |
| C、为0 | D、与a的取值有关 |
考点:函数的值
专题:函数的性质及应用
分析:根据题意,设g(x)=log2(
-5x),x∈R,得出g(x)是奇函数;由ln
=-lna,计算f(lna)+f(ln
)即可.
| 1+25x2 |
| 1 |
| a |
| 1 |
| a |
解答:
解:根据题意,设g(x)=log2(
-5x),x∈R;
∴g(-x)=log2(
+5x)
=log2
=-log2(
-5x)
=-g(x);
∴g(x)是定义域R上的奇函数;
∴f(x)=g(x)+3;
又∵ln
=-lna,
∴f(lna)+f(ln
)=f(lna)+f(-lna)
=[g(lna)+3]+[g(-lna)+3]
=[g(lna)+g(-lna)]+6
=6.
故选:B.
| 1+25x2 |
∴g(-x)=log2(
| 1+25x2 |
=log2
| 1 | ||
|
=-log2(
| 1+25x2 |
=-g(x);
∴g(x)是定义域R上的奇函数;
∴f(x)=g(x)+3;
又∵ln
| 1 |
| a |
∴f(lna)+f(ln
| 1 |
| a |
=[g(lna)+3]+[g(-lna)+3]
=[g(lna)+g(-lna)]+6
=6.
故选:B.
点评:本题考查了函数的奇偶性的应用问题,解题时应根据函数的奇偶性,灵活地利用g(lna)+g(-lna)=0这一结论,是基础题.

练习册系列答案
相关题目
设函数y=f(x)对任意的x∈R满足f(4+x)=f(-x),当x∈(-∞,2]时,有f(x)=2-x-5.若函数f(x)在区间(k,k+1)(k∈Z)上有零点,则k的值为( )
| A、-3或7 | B、-4或7 |
| C、-4或6 | D、-3或6 |
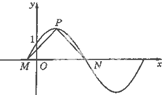 如图,函数y=2sin(πx+φ),x∈R(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R(其中0≤φ≤| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
某奶茶店为了了解奶茶销售量与气温之间的关系,随机统计并制作了6天卖出的奶茶的杯数与气温的对照表:
经检验,这组样本数据具有线性相关关系,那么,对于气温x(℃)与奶茶销售量y这两个变量,下列判断正确的是( )
| 气温x(℃) | 26 | 19 | 14 | 10 | 4 | -1 |
| 杯数y | 201 | 242 | 339 | 383 | 505 | 640 |
| A、成正相关,其回归直线经过点(13,385) |
| B、成负相关,其回归直线经过点(13,386) |
| C、成正相关,其回归直线经过点(12,386) |
| D、成负相关,其回归直线经过点(12,385) |
 一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是( )海里.
一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是( )海里.A、30(
| ||||
B、30(
| ||||
C、30(
| ||||
D、30(
|