题目内容
(
-
) n的展开式中只有第3项的二项式系数最大,则它的x-3项的系数是 .
| x |
| 2 |
| x2 |
考点:二项式定理的应用
专题:计算题,二项式定理
分析:由二项式系数的性质,可得n为偶数,即有
+1=3,解得n=4,求出(
-
) n的展开式的通项公式,化简整理,再令x的指数为-3,即可得到所求的系数.
| n |
| 2 |
| x |
| 2 |
| x2 |
解答:
解:由二项式系数的性质,可得n为偶数,
且有中间项的二项式系数最大,即有
+1=3,
解得,n=4,
则(
-
) n的展开式的通项公式Tr+1=
(
)4-r(-
)r
=
(-2)rx
,
令
=-3,解得,r=2.
则它的x-3项的系数是
(-2)2=24,
故答案为:24
且有中间项的二项式系数最大,即有
| n |
| 2 |
解得,n=4,
则(
| x |
| 2 |
| x2 |
| C | r 4 |
| x |
| 2 |
| x2 |
=
| C | r 4 |
| 4-5r |
| 2 |
令
| 4-5r |
| 2 |
则它的x-3项的系数是
| C | 2 4 |
故答案为:24
点评:本题考查二项式系数的性质和二项式展开式的通项及运用,考查运算能力,属于中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
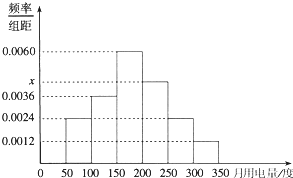 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.求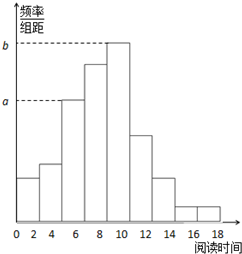 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: