题目内容
10.已知x∈R,符号[x]表示不超过x的最大整数,如[1.9]=1,[2.01]=2.若函数$f(x)=\frac{x}{[x]}-m$(x≥1)有且仅有三个零点,则m的取值范围是( )| A. | $[{\frac{3}{2},2}]$ | B. | $[{\frac{3}{2},2})$ | C. | $[{\frac{5}{4},\frac{4}{3}})$ | D. | $[{\frac{5}{4},\frac{4}{3}}]$ |
分析 由f(x)=0得 $\frac{x}{[x]}$=m,令g(x)=$\frac{x}{[x]}$,作出g(x)的图象,利用数形结合即可得到a的取值范围.
解答 解:由f(x)=$\frac{x}{[x]}$-m=0得:$\frac{x}{[x]}$=m,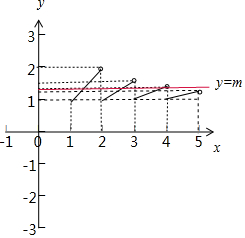
当1≤x<2,[x]=1,此时g(x)=x,此时1≤g(x)<2,
当2≤x<3,[x]=2,此时g(x)=$\frac{1}{2}x$,此时1≤g(x)<$\frac{3}{2}$,
当3≤x<4,[x]=3,此时g(x)=$\frac{1}{3}x$,此时≤1g(x)<$\frac{4}{3}$,
当4≤x<5,[x]=4,此时g(x)=$\frac{1}{4}$x,此时1≤g(x)<$\frac{5}{4}$,
作出函数g(x)的图象,
要使函数$f(x)=\frac{x}{[x]}-m$(x≥1)有且仅有三个零点,
即函数g(x)=m有且仅有三个零点,
则由图象可知$\frac{5}{4}$≤m$<\frac{4}{3}$,
故选:C.
点评 本题主要考查函数零点的应用,根据函数和方程之间的关系构造函数g(x),利用数形结合是解决本题的关键.难度较大.

练习册系列答案
相关题目
20.甲、乙两个人投篮,他们投进篮的概率分别为$\frac{2}{5},\frac{1}{2}$,现甲、乙两人各投篮1次,则两个人都投进的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{4}{5}$ |
5.命题“?x∈R,x2-4x+4≥0”的否定是( )
| A. | ?x∈R,x2-4x+4<0 | B. | ?x∉R,x2-4x+4<0 | ||
| C. | $?{x_0}∈R,{x_0}^2-4{x_0}+4<0$ | D. | $?{x_0}∉R,{x_0}^2-4{x_0}+4<0$ |
3.已知抛物线C:y2=4x的交点为F,直线y=x-1与C相交于A,B两点,与双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=2(a>0,b>0)的渐近线相交于M,N两点,若线段AB与MN的中点相同,则双曲线E离心率为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | 2 | C. | $\frac{\sqrt{15}}{3}$ | D. | $\sqrt{3}$ |
