题目内容
7.已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$一个周期的图象如图所示,则φ的值为( )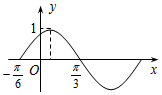
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{8}$ |
分析 由函数f(x)=Asin(ωx+φ)的图象可得A=1,$\frac{T}{2}$=$\frac{π}{2}$,T=π,ω=2,由特殊点的坐标求出φ的值.
解答 解:由函数f(x)=Asin(ωx+φ)的图象可得A=1,$\frac{T}{2}$=$\frac{π}{2}$,T=π,ω=2
再根据图象过点($\frac{π}{12}$,1),
可得sin($\frac{π}{6}$+φ)=1,结合|φ|<$\frac{π}{2}$,可得φ=$\frac{π}{3}$.
故选C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由特殊点的坐标求出φ的值,再根据五点法作图求出ω的值,属于基础题.

练习册系列答案
相关题目
17.下列命题中正确的是( )
| A. | 若p:?x∈R,ex>xe,q:?x0∈R,|x0|≤0,则(¬p)∧q为假 | |
| B. | x=1是x2-x=0的必要不充分条件 | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
12.设a,b是两条不同的直线,α,β是两个不同的平面,则下列四个命题错误的是( )
| A. | 若a⊥b,a⊥α,b?α,则b∥α | B. | 若a⊥b,a⊥α,b⊥β,则α⊥β | ||
| C. | 若a⊥β,α⊥β,则a∥α或a?α | D. | 若a∥α,α⊥β,则a⊥β |
16.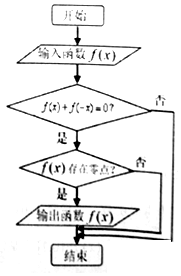 程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )
程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )
 程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )
程序框图如图所示,现输入如下四个函数:f(x)=$\frac{1}{x}$,f(x)=x4,f(x)=2x,f(x)=x-$\frac{1}{x}$,则可以输出的函数是( )| A. | f(x)=$\frac{1}{x}$ | B. | f(x)=x4 | C. | f(x)=2x | D. | f(x)=x-$\frac{1}{x}$ |
