题目内容
20.已知角α为第四象限角,且$tanα=-\frac{4}{3}$(1)求sinα+cosα的值;
(2)求$\frac{sin(π-α)+2cos(π+α)}{{sin(\frac{3}{2}π-α)-cos(\frac{3}{2}π+α)}}$的值.
分析 (1)由已知利用同角三角函数基本关系式可求sinα,cosα的值,即可得解;
(2)利用诱导公式,同角三角函数基本关系式化简所求即可计算得解.
解答 解:(1)因为角α为第四象限角,且$tanα=-\frac{4}{3}$,
∴$sinα=-\frac{4}{5},cosα=\frac{3}{5}$,…(4分)
则$sinα+cosα=-\frac{1}{5}$.…(5分)
(2)原式=$\frac{sinα-2cosα}{-cosα-sinα}=\frac{tanα-2}{-1-tanα}=\frac{{-\frac{4}{3}-2}}{{-1+\frac{4}{3}}}=\frac{{-\frac{10}{3}}}{{\frac{1}{3}}}=-10$.…(10分)
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.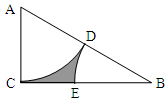 如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
 如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,AB=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BDE,D在AB上,E在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | 1-$\frac{{\sqrt{3}π}}{6}$ | B. | $\frac{{\sqrt{3}π}}{6}$ | C. | 1-$\frac{π}{4}$ | D. | $\frac{π}{4}$ |
8.一个棱长为4的正方体涂上红色后,将其切成棱长为1的小正方体,置于一密闭容器搅拌均匀,从中任取一个,则取到两面涂红色的小正方体的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{8}{27}$ | D. | $\frac{12}{27}$ |
5.已知函数f(x)是定义在[0,+∞)上的增函数,则满足不等式f(2x-1)<f($\frac{1}{3}$)的实数x的取值范围是( )
| A. | (-∞,$\frac{2}{3}$) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,$\frac{2}{3}$) |
12.设a,b是两条不同的直线,α,β是两个不同的平面,则下列四个命题错误的是( )
| A. | 若a⊥b,a⊥α,b?α,则b∥α | B. | 若a⊥b,a⊥α,b⊥β,则α⊥β | ||
| C. | 若a⊥β,α⊥β,则a∥α或a?α | D. | 若a∥α,α⊥β,则a⊥β |
9.已知一个水平放置的正方形用斜二测画法作出的直观图是一个平行四边形,若平行四边形中有一条边为4,则此正方形的面积是( )
| A. | .16或36 | B. | 36或64 | C. | 16或64 | D. | 36 |
13.若等差数列{an}的公差为d,前n项和为Sn,记bn=$\frac{{S}_{n}}{n}$,则( )
| A. | 数列{bn}是等差数列,{bn}的公差也为d | |
| B. | 数列{bn}是等差数列,{bn}的公差为2d | |
| C. | 数列{an+bn}是等差数列,{an+bn}的公差为d | |
| D. | 数列{an-bn}是等差数列,{an-bn}的公差为$\frac{d}{2}$ |
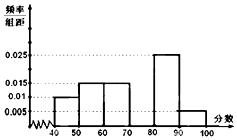 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: