题目内容
5.函数f(x)=ln|x-1|+2cosπx(-2≤x≤4)的所有零点之和等于( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 函数f(x)=ln|x-1|+2cosπx的零点,即为函数f(x)=2cosπx与函数g(x)=ln|x-1|的图象交点的横坐标,由图象变化的法则和余弦函数的特点作出函数的图象,由对称性可得答案.
解答 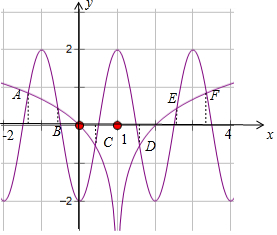 解:f(x)=ln|x-1|+2cosπx的零点,
解:f(x)=ln|x-1|+2cosπx的零点,
即为函数f(x)=-2cosπx与函数g(x)=ln|x-1|的图象交点的横坐标,
由图象变化的法则可知:y=ln|x-1|的图象作关于y轴的对称后和原来的一起构成y=ln|x|的图象,
在向右平移1个单位得到y=ln|x-1|的图象
又f(x)=-2cosπx的周期为2,如图所示:
两图象都关于直线x=1对称,且共有A,B,C,D,E,F,6个交点,
由中点坐标公式可得:xA+xF=2,xB+xE=2,xC+xD=2,
故所有交点的横坐标之和为6,
故选:C.
点评 本题考查函数图象的作法,熟练作出函数的图象是解决问题的关键,属中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15.已知向量$\overrightarrow a=({m,1}),\overrightarrow b=({1,n-2}),({m>0,n>0})$若$\overrightarrow a⊥\overrightarrow b$,则$\frac{1}{m}+\frac{2}{n}$的最小值为( )
| A. | 2$\sqrt{2}$ | B. | $\frac{3}{2}$+$\sqrt{2}$ | C. | 3$\sqrt{2}$+2 | D. | 2$\sqrt{2}$+3 |
16.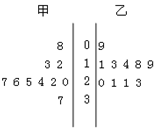 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )
 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个,命中个数的茎叶图如图所示,则下列结论错误 的一个是( )| A. | 甲的极差是29 | B. | 甲的中位数是25 | ||
| C. | 乙的众数是21 | D. | 甲的平均数比乙的大 |
20.甲、乙两个人投篮,他们投进篮的概率分别为$\frac{2}{5},\frac{1}{2}$,现甲、乙两人各投篮1次,则两个人都投进的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{4}{5}$ |
17.下列命题中正确的是( )
| A. | 若p:?x∈R,ex>xe,q:?x0∈R,|x0|≤0,则(¬p)∧q为假 | |
| B. | x=1是x2-x=0的必要不充分条件 | |
| C. | 直线ax+y+2=0与ax-y+4=0垂直的充要条件为a=±1 | |
| D. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” |
14.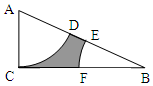 如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
 如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )
如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( )| A. | $\frac{π}{8}$ | B. | 1-$\frac{π}{8}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
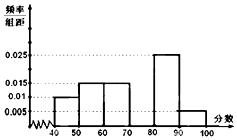 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题: