题目内容
在△ABC中，内角A、B、C的对边分别为a，b，c，且a、b、c成等比数列．
（Ⅰ）若cosB=
，求
+
的值；
（Ⅱ）若△ABC的周长为6，求△ABC的面积的最大值．
（Ⅰ）若cosB=
| 1 |
| 3 |
| 1 |
| tanA |
| 1 |
| tanC |
（Ⅱ）若△ABC的周长为6，求△ABC的面积的最大值．
考点：正弦定理,同角三角函数基本关系的运用
专题：解三角形
分析：（Ⅰ）利用△ABC中，a、b、c成等比数列及正弦定理可得sin2B=sinAsinC，再结合cosB=
，将所求关系式中的切化弦即可求得其值；
（Ⅱ）利用余弦定理及基本不等式可求得cosB≥
，B∈（0，
]，6=a+b+c=
+a+c≥3
⇒ac≤4，从而可求得△ABC的面积的最大值．
| 1 |
| 3 |
（Ⅱ）利用余弦定理及基本不等式可求得cosB≥
| 1 |
| 2 |
| π |
| 3 |
| ac |
| ac |
解答：
解：（Ⅰ）由a、b、c成等比数列，得b2=ac，sin2B=sinAsinC----（2分）
又cosB=
，得sinB=
（0＜B＜π）-----------------------------（3分）
+
=
+
---------------------------------------（4分）
=
-------------------------------------（5分）
=
=
------------------------------------------（6分）
（Ⅱ）cosB=
≥
=
，-------------------------（7分）
∴B∈（0，
]，∴sinB≤
--------------------------------（8分）
又6=a+b+c=
+a+c≥3
（当且仅当a=c=2时取“=”）------------（9分）
∴ac≤4，（10分）
∴S△ABC=
acsinB≤
×4×
=
--------------------（11分）
∴S△ABC的最大值为
---------------（12分）（文科）
又cosB=
| 1 |
| 3 |
2
| ||
| 3 |
| 1 |
| tanA |
| 1 |
| tanC |
| cosA |
| sinA |
| cosC |
| sinC |
=
| sin(A+C) |
| sinAsinC |
=
| 1 |
| sinB |
3
| ||
| 4 |
（Ⅱ）cosB=
| a2+c2-b2 |
| 2ac |
| ac |
| 2ac |
| 1 |
| 2 |
∴B∈（0，
| π |
| 3 |
| ||
| 2 |
又6=a+b+c=
| ac |
| ac |
∴ac≤4，（10分）
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴S△ABC的最大值为
| 3 |
点评：本题考同角三角函数基本关系的运用，着重考查正弦定理与余弦定理及基本不等式的综合应用，考查运算求解能力，属于中档题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
已知函数f（x）是定义在R上的奇函数，对任意x，y∈R，x+y≠0，都有
＞0，若x＞2y，则（ ）
| f(x)+f(y) |
| x+y |
| A、f（x）＞f（2y） |
| B、f（x）≥f（2y） |
| C、f（x）＜f（2y） |
| D、f（x）≤f（2y） |
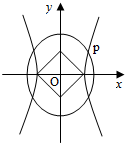如图，O为坐标原点，双曲线C1：
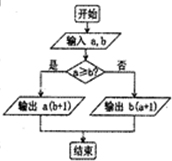如图，定义某种运算S=a?b，运算原理如图所示，则式子（2tan