题目内容
13．
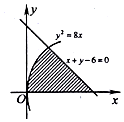如图，由抛物线y2=8x与直线x+y-6=0及x轴所围成的图形（图中阴影部分）的面积为$\frac{40}{3}$．
分析 根据定积分的定义结合图象可得S=${∫}_{0}^{2}$2$\sqrt{2}$•$\sqrt{x}$dx+${∫}_{2}^{6}$（6-x）dx，然后利用定积分的定义进行计算
解答 解：由$\left\{\begin{array}{l}{{y}^{2}=8x}\\{x+y-6=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$．
由x+y-6=0，令y=0，解得x=6，
设所求图形面积为S=${∫}_{0}^{2}$2$\sqrt{2}$•$\sqrt{x}$dx+${∫}_{2}^{6}$（6-x）dx=$\frac{4}{3}$•$\sqrt{2}$${x}^{\frac{3}{2}}$|${\;}_{0}^{2}$+（6x-$\frac{1}{2}$x2）|${\;}_{2}^{6}$=$\frac{16}{3}$+8=$\frac{40}{3}$，
故答案为：$\frac{40}{3}$．
点评 此题考查利用定积分求图形的面积问题，解题的关键是将图象的面积分为两部分进行处理．
练习册系列答案
相关题目
4．设F1，F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的两个焦点，点P在双曲线上，已知|PF1|是|PF2|和|F1F2|的等差中项，且∠F1PF2=120°，则该双曲线的离心率为（ ）
| A． | 1 | B． | $\frac{3}{2}$ | C． | $\frac{5}{2}$ | D． | $\frac{7}{2}$ |
8．已知a∈R，则“a＜3”是“|x+2|+|x-1|＞a恒成立”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
5．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{4}$=1的右焦点到该双曲线渐近线的距离等于（ ）
| A． | 4 | B． | 3 | C． | 2$\sqrt{2}$ | D． | 2 |
3．函数y=lg（cosx-$\frac{\sqrt{3}}{2}$）的定义域为（ ）
| A． | （-$\frac{π}{6}$，$\frac{π}{6}$） | B． | （kπ-$\frac{π}{6}$，kπ+$\frac{π}{6}$）（k∈π） | ||
| C． | （2kπ-$\frac{π}{6}$，2kπ+$\frac{π}{6}$）（k∈Z） | D． | R |