题目内容
2.在△ABC中,角B为钝角,则sinB>sin(A+B).(填“>”或“<”或“=”)分析 由B为钝角,A为锐角,可得0<sinA<1,cosB<0,0<cosA<1,0<sinB<1,利用两角和的正弦函数公式,做差即可计算得解.
解答 解:∵sin(A+B)=sinAcosB+cosAsinB,
又∵B为钝角,A为锐角,
∴0<sinA<1,cosB<0,0<cosA<1,0<sinB<1,
∴sinB-sin(A+B)=sinB(1-cosA)-sinAcosB>0,即sinB>sin(A+B),
故答案为:>.
点评 此题考查了三角函数值的符号,两角和的正弦函数公式,熟练掌握公式及性质是解本题的关键,属于基础题.

练习册系列答案
相关题目
17.设a,b∈(0,+∞),则“a>b”是“logab<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下:
5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
(Ⅰ)写出m,n的值,若该“微信运动”团队共有120人,请估计该团队中一天行走步数不少于7500步的人数;
(Ⅱ)记C组步数数据的平均数与方差分别为v1,$s_1^2$,E组步数数据的平均数与方差分别为v2,$s_2^2$,试分别比较v1与v2,$s_1^2$与$s_2^2$的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的步数数据中任取2个数据,求这2个数据步数差的绝对值大于3000步的概率.
5860 6520 7326 6798 7325
8430 8215 7453 7446 6754
7638 6834 6460 6830 9860
8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为x)
| 组别 | 步数分组 | 频数 |
| A | 5500≤x<6500 | 2 |
| B | 6500≤x<7500 | 10 |
| C | 7500≤x<8500 | m |
| D | 8500≤x<9500 | 2 |
| E | 9500≤x<10500 | n |
(Ⅱ)记C组步数数据的平均数与方差分别为v1,$s_1^2$,E组步数数据的平均数与方差分别为v2,$s_2^2$,试分别比较v1与v2,$s_1^2$与$s_2^2$的大小;(只需写出结论)
(Ⅲ)从上述A,E两个组别的步数数据中任取2个数据,求这2个数据步数差的绝对值大于3000步的概率.
11.下列函数中为奇函数的是( )
| A. | y=x2+2x | B. | y=ln|x| | C. | y=($\frac{1}{3}$)x | D. | y=xcosx |
12.已知函数f(x)=$\left\{\begin{array}{l}{-\frac{3x+2}{x+1},x∈(-1,0]}\\{x,x∈(0,1]}\end{array}\right.$且g(x)=mx+m,若g(x)=f(x)在(-1,1]内有且仅有两个不同的根,则实数m的取值范围是( )
| A. | (-$\frac{9}{4}$,-2]∪(0,$\frac{1}{2}$] | B. | (-$\frac{11}{4}$,-2]∪(0,$\frac{1}{2}$] | C. | (-$\frac{9}{4}$,-2]∪(0,$\frac{2}{3}$] | D. | (-$\frac{11}{4}$,-2]∪(0,$\frac{2}{3}$] |
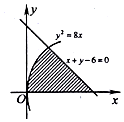 如图,由抛物线y2=8x与直线x+y-6=0及x轴所围成的图形(图中阴影部分)的面积为$\frac{40}{3}$.
如图,由抛物线y2=8x与直线x+y-6=0及x轴所围成的图形(图中阴影部分)的面积为$\frac{40}{3}$.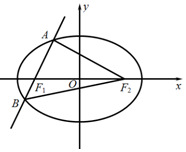 如图,已知F1、F2是椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,直线l:y=k(x+1)经过左焦点F1,且与椭圆G交于A、B两点,△ABF2的周长为$4\sqrt{3}$.
如图,已知F1、F2是椭圆G:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点,直线l:y=k(x+1)经过左焦点F1,且与椭圆G交于A、B两点,△ABF2的周长为$4\sqrt{3}$.