复数是纯虚数.则实数a=2．题目和参考答案——青夏教育精英家教网——

题目内容

1．复数（a+i）（1+2i）是纯虚数（i是虚数单位），则实数a=2．

分析直接由复数代数形式的乘除运算化简，再由实部等于0且虚部不等于0求解即可得答案．

解答解：∵（a+i）（1+2i）=a-2+（1+2a）i是纯虚数，
∴$\left\{\begin{array}{l}{a-2=0}\\{1+2a≠0}\end{array}\right.$，解得a=2．
故答案为：2．

点评本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案

一诺书业暑假作业快乐假期云南美术出版社系列答案

假日氧吧快乐假日精彩生活系列答案

超能学典口算题卡系列答案

学考单元练测卷系列答案

小学期末总冲刺系列答案

步步高系列衔接教材精华课堂暑假天天乐西安出版社系列答案

中考必考名著精讲细练系列答案

特训30天衔接教材武汉出版社系列答案

好学生口算心算速算系列答案

书立方地方专版系列答案

相关题目

11．在100个球中有红球20个，从中抽取10个球进行分析，如果用分层抽样的方法对其进行抽样，则应抽取红球（　　）

12．已知函数f（x）=e^x-ax+a（a∈R），其中e为自然对数的底数．
（1）讨论函数y=f（x）的单调性；
（2）函数y=f（x）的图象与x轴交于A（x₁，0），B（x₂，0）两点，x₁＜x₂，点C在函数y=f（x）的图象上，且△ABC为等腰直角三角形，记$\sqrt{\frac{{{x_2}-1}}{{{x_1}-1}}}=t$，求at-（a+t）的值．

9．设等差数列{a_n}的前n项和为S_n，若S_n有最大值，且$\frac{{a}_{9}}{{a}_{8}}$＜-1，则S_n取得最小正值时，n=（　　）

16．设命题p：?x∈（-∞，0），2^x＜x²，则￢p为（　　）

	A．	$?{x_0}∈[{0，+∞}），{2^{x_0}}≥{x_0}^2$		B．	$?{x_0}∈（{-∞，0}），{2^{x_0}}≥{x_0}^2$
	C．	?x∈（-∞，0），2^x≥x²		D．	?x∈[0，+∞），2^x＜x²

6．已知a，b＞0，且a+b=1，求证：$\sqrt{a+1}+\sqrt{b+1}≤\sqrt{6}$．

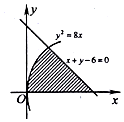如图，由抛物线y²=8x与直线x+y-6=0及x轴所围成的图形（图中阴影部分）的面积为$\frac{40}{3}$．

10．已知定义在R上的奇函数y=f（x）的图象关于直线x=1对称，当-1≤x＜0时，f（x）=-log${\;}_{\frac{1}{2}}$（-x），则方程f（x）-$\frac{1}{2}$=0在（0，6）内的所有根之和为12．

11．下列函数中为奇函数的是（　　）

y=（$\frac{1}{3}$）^x