题目内容
在边长为1的正六边形ABCDEF中，记以A为起点，其余顶点为终点的向量分别为
，
，
，
，
；以D为起点，其余顶点为终点的向量分别为
，
，
，
，
．记m=（
+
+
）•（
+
+
），其中{i，j，k}⊆{1，2，3，4，5}，{r，s，t}⊆{1，2，3，4，5}，则m的最小值= ．
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
| d1 |
| d2 |
| d3 |
| d4 |
| d5 |
| ai |
| aj |
| ak |
| dr |
| ds |
| dt |
考点：空间向量的数量积运算
专题：平面向量及应用
分析：由已知可得当
，
，
分别对应向量
，
，
，
，
，
分别对应向量
，
，
时，m=（
+
+
）•（
+
+
）取最小值，进而求出答案．
| ai |
| aj |
| ak |
| AC |
| AD |
| AE |
| dr |
| ds |
| dt |
| DF |
| DA |
| DB |
| ai |
| aj |
| ak |
| dr |
| ds |
| dt |
解答：
解：如图所示：
∵以A为起点，其余顶点为终点的向量分别为
，
，
，
，
；
以D为起点，其余顶点为终点的向量分别为
，
，
，
，
．
{i，j，k}⊆{1，2，3，4，5}，{r，s，t}⊆{1，2，3，4，5}，
可知i，j，k互不相等，r，s，t互不相等，
故当
，
，
分别对应向量
，
，
，
，
，
分别对应向量
，
，
时，
m=（
+
+
）•（
+
+
）取最小值，
此时|
+
+
|=|
+
+
|=5，
且＜
+
+
，
+
+
＞=180，
故此时m=-25，
即m的最小值为-25，
故答案为：-25
∵以A为起点，其余顶点为终点的向量分别为
| a1 |
| a2 |
| a3 |
| a4 |
| a5 |
以D为起点，其余顶点为终点的向量分别为
| d1 |
| d2 |
| d3 |
| d4 |
| d5 |
{i，j，k}⊆{1，2，3，4，5}，{r，s，t}⊆{1，2，3，4，5}，
可知i，j，k互不相等，r，s，t互不相等，
故当
| ai |
| aj |
| ak |
| AC |
| AD |
| AE |
| dr |
| ds |
| dt |
| DF |
| DA |
| DB |
m=（
| ai |
| aj |
| ak |
| dr |
| ds |
| dt |
此时|
| ai |
| aj |
| ak |
| dr |
| ds |
| dt |
且＜
| ai |
| aj |
| ak |
| dr |
| ds |
| dt |
故此时m=-25，
即m的最小值为-25，
故答案为：-25
点评：本题考查的知识点是向量数量积，其中分析出当
，
，
分别对应向量
，
，
，
，
，
分别对应向量
，
，
时，m=（
+
+
）•（
+
+
）取最小值，是解答的关键．
| ai |
| aj |
| ak |
| AC |
| AD |
| AE |
| dr |
| ds |
| dt |
| DF |
| DA |
| DB |
| ai |
| aj |
| ak |
| dr |
| ds |
| dt |
练习册系列答案
相关题目
（理科）
tan21°tan39°-tan159°+tan39°=（ ）
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
cosα+cosβ=
，sinα+sinβ=
，则cos（α-β ）=（ ）
| 1 |
| 2 |
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
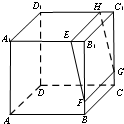如图，平面EFGH为长方体ABCD-A1B1C1D1的截面，E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，EH∥A1D1，则四边形EFGH的形状是（ ）