题目内容

某次越野赛跑有两个队参加，每队有5名选手参加，规定一个选手第n个跑完就为他的队得n分，总分少的队得胜，若没有两个选手同时跑完，则胜队的总分的种数可能是
 
．
考点：计数原理的应用
专题：排列组合
分析：获胜队最少总分为1+2+3+4+5=15（分）；总分是1+2+…+10=55（分）；获胜队最多分数为27分；找出从15分～27分之间的可能情况即可．
解答： 解：获胜队最少总分为1+2+3+4+5=15（分）；
总分是1+2+…+10=55（分）；
55÷2=27.5（分）；
获胜队最多分数为27分；
获胜队的得分应该有：
27-15+1=13（种）；
故答案为：13．
点评：本题先找出获胜队得分的范围，再根据这个范围找出可能情况．
练习册系列答案
相关题目
函数f（x）由下表定义：
x 2 5 3 1 4
f（x） 1 2 3 4 5
若a0=5，an+1=f（an），n=0，1，2，…，则a2013=
 
．
已知函数f（x）=
cosx
2sinx
+
sin
x
2
•cos
x
2
2cos2
x
2
-1
，则f（
π
8
）=
 
．
复数z满足（1+2i）z=4+3i，则z的共轭复数
.
z
=
 
．
在边长为1的正六边形ABCDEF中，记以A为起点，其余顶点为终点的向量分别为
a1
，
a2
，
a3
，
a4
，
a5
；以D为起点，其余顶点为终点的向量分别为
d1
，
d2
，
d3
，
d4
，
d5
．记m=（
ai
+
aj
+
ak
）•（
dr
+
ds
+
dt
），其中{i，j，k}⊆{1，2，3，4，5}，{r，s，t}⊆{1，2，3，4，5}，则m的最小值=
 
．
若a，b，c为实数，则下列不等式恒成立的是（　　）
A、若a＞b，则ac2＞bc2
B、若a＞b，则
1
a
＜
1
b
C、若a＜b，则a2＜b2
D、若a+c＞b+c，则a＞b
在等差数列{an}中，a1+a9=10，则a2+a8的值为（　　）
A、5B、6C、8D、10
设i是虚数单位，复数
a+3i
1-2i
（a∈R）是纯虚数，则实数a的值是（　　）
A、-6B、-2C、6D、4
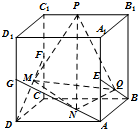已知点E、F、G分别是正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点，点M、N、Q、P分别在线段DF、AG、BE、C1B1上．以M、N、Q、P为顶点的三棱锥P-MNQ的俯视图不可能是（　　）
A、
B、
C、
D、

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网