题目内容
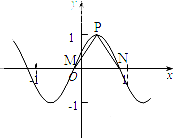 已知函数f(x)=
已知函数f(x)=
| ||
| 2 |
| 1 |
| 2 |
| PM |
| PN |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质,平面向量及应用
分析:由已知,f(x)=
sinπx+
cosπx=sin(πx+
).根据三角函数的图象与性质分别求出M,N,P坐标,得出
=(-
,-1),
=(
,-1),再利用向量数量积公式变形得出夹角的余弦值.
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| PM |
| 1 |
| 2 |
| PN |
| 1 |
| 2 |
解答:
解:f(x)=
sinπx+
cosπx=sin(πx+
),
由f(x)=0,得出πx+
=kπ,k∈Z,
取k=0得x=-
所以M(-
,0),
取k=1得x=
所以N(
,0),
由f(x)=1,x∈[-1,1],得πx+
=
,x=
,所以P(
,1),
∴
=(-
,-1),
=(
,-1),
cosθ=
=
=
.
故选:D.
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
由f(x)=0,得出πx+
| π |
| 6 |
取k=0得x=-
| 1 |
| 6 |
| 1 |
| 6 |
取k=1得x=
| 5 |
| 6 |
| 5 |
| 6 |
由f(x)=1,x∈[-1,1],得πx+
| π |
| 6 |
| π |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
∴
| PM |
| 1 |
| 2 |
| PN |
| 1 |
| 2 |
cosθ=
| ||||
|
|
| ||||||||
|
| 3 |
| 5 |
故选:D.
点评:本题考查向量数量积、夹角的计算,考查了三角恒等变换、三角函数图象与性质.考查转化、计算能力,属于中档题.

练习册系列答案
相关题目
设a>0,f(x)=ex-
在任一点处的切线的倾斜角的取值范围是[
,
),则a=( )
| a |
| ex |
| π |
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
| C、3 | ||
D、
|
已知定义域为R的函数f(x)满足f(-x)=-f(x+4),且函数f(x)在区间(2,+∞)上单调递增.如果x1<2<x2,且x1+x2<4,则f(x1)+f(x2)的值( )
| A、可正可负 | B、恒大于0 |
| C、可能为0 | D、恒小于0 |
当参数θ变化时,动点P(2cosθ,3sinθ)所确定的曲线为( )
| A、直线 | B、圆 | C、椭圆 | D、双曲线 |
已知点F1(-10,0)、F2(10,0),P是双曲线
-
=1上的一点,则|PF1|-|PF2|=( )
| x2 |
| 36 |
| y2 |
| 64 |
| A、12 | B、-12 |
| C、-12或12 | D、16或12 |