题目内容
定义函数f(x)=
,以下几个命题中:
①存在实数a,使f(a)•f(-a)=1;
②任意a,b∈R,都有f(a2)+f(b2)≥2f(ab);
③存在实数a,b,使f(a)+f(b)=f(ab);
④任意a,b∈R,都有f(a)•f(b)≥f(a+b)
正确的命题个数为( )
|
①存在实数a,使f(a)•f(-a)=1;
②任意a,b∈R,都有f(a2)+f(b2)≥2f(ab);
③存在实数a,b,使f(a)+f(b)=f(ab);
④任意a,b∈R,都有f(a)•f(b)≥f(a+b)
正确的命题个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①取a=0,则f(0)=1,满足条件;
②任意a,b∈R,都有f(a2)+f(b2)=ea2+eb2≥2ea2+b2≥2e2|ab|
分类讨论ab<0,ab≥0,即可得出;
③假设a>0,b>0,取eb=
,满足f(a)+f(b)=f(ab);
④任意a,b∈R,分类讨论:当ab=0时;当ab<0时;当a>0,b>0时;当a<0,b<0时.即可判断出.
②任意a,b∈R,都有f(a2)+f(b2)=ea2+eb2≥2ea2+b2≥2e2|ab|
分类讨论ab<0,ab≥0,即可得出;
③假设a>0,b>0,取eb=
| ea |
| ea-1 |
④任意a,b∈R,分类讨论:当ab=0时;当ab<0时;当a>0,b>0时;当a<0,b<0时.即可判断出.
解答:
解:①存在实数a,使f(a)•f(-a)=1,正确,例如取a=0,则f(0)=1;
②任意a,b∈R,都有f(a2)+f(b2)=ea2+eb2≥2ea2+b2≥2e2|ab|
若ab<0,则f(a2)+f(b2)≥2e>1,成立,
若ab≥0,则f(a2)+f(b2)≥2e2ab>2eab=2f(ab).
综上可知正确.
③假设a>0,b>0,取eb=
,则f(a)+f(b)=ea+
=eab=f(ab);
④任意a,b∈R,
当ab=0时,则f(a)f(b)=f(0)f(b)=f(b)=f(a+b),因此f(a)•f(b)≥f(a+b)成立;
当ab<0时,不妨设a>0>b,则f(a)•f(b)=f(a)>f(a+b),因此f(a)•f(b)≥f(a+b)成立;
当a>0,b>0时,f(a)•f(b)=ea+b=f(a+b),成立;
当a<0,b<0时,f(a)f(b)=1=f(a+b).
综上可知:都有f(a)•f(b)≥f(a+b)
即正确的命题个数为4.
故选:D.
②任意a,b∈R,都有f(a2)+f(b2)=ea2+eb2≥2ea2+b2≥2e2|ab|
若ab<0,则f(a2)+f(b2)≥2e>1,成立,
若ab≥0,则f(a2)+f(b2)≥2e2ab>2eab=2f(ab).
综上可知正确.
③假设a>0,b>0,取eb=
| ea |
| ea-1 |
| ea |
| ea-1 |
④任意a,b∈R,
当ab=0时,则f(a)f(b)=f(0)f(b)=f(b)=f(a+b),因此f(a)•f(b)≥f(a+b)成立;
当ab<0时,不妨设a>0>b,则f(a)•f(b)=f(a)>f(a+b),因此f(a)•f(b)≥f(a+b)成立;
当a>0,b>0时,f(a)•f(b)=ea+b=f(a+b),成立;
当a<0,b<0时,f(a)f(b)=1=f(a+b).
综上可知:都有f(a)•f(b)≥f(a+b)
即正确的命题个数为4.
故选:D.
点评:本题考查了分类讨论和指数函数的单调性,属于中档题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、“a>b”是“a2>b2”的必要条件 |
| B、自然数的平方大于0 |
| C、存在一个钝角三角形,它的三边长均为整数 |
| D、“若a,b都是偶数,则a+b是偶数”的否命题为真 |
已知变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、3 | B、4 | C、6 | D、7 |
设变量x,y满足约束条件
,则目标函数z=x+5y的最大值为( )
|
| A、2 | B、3 | C、4 | D、5 |
已知两个变量x,y之间具有线性相关关系,试验测得(x,y)的四组值分别为(1,2),(2,4),(3,5),(4,7),则y与x之间的回归直线方程为( )
| A、y=0.8x+3 |
| B、y=-1.2x+7.5 |
| C、y=1.6x+0.5 |
| D、y=1.3x+1.2 |
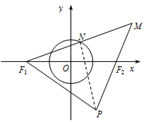 如图,已知定点F1(-2,0),F2(2,0),动点N满足|
如图,已知定点F1(-2,0),F2(2,0),动点N满足|