题目内容
15．已知a=${∫}_{0}^{1}$xdx，b=${∫}_{0}^{1}$x2dx，c=${∫}_{0}^{1}$$\sqrt{x}$dx，则a，b，c的大小关系是（ ）| A． | a＜b＜c | B． | a＜c＜b | C． | b＜a＜c | D． | c＜a＜b |
分析 根据定积分的计算法则，分别求出a，b，c，再比较即可．
解答 解：a=${∫}_{0}^{1}$xdx=$\frac{1}{2}{x}^{2}$|${\;}_{0}^{1}$=$\frac{1}{2}$，b=${∫}_{0}^{1}$x2dx=$\frac{1}{3}{x}^{3}$|${\;}_{0}^{1}$=$\frac{1}{3}$，c=${∫}_{0}^{1}$$\sqrt{x}$dx=$\frac{2}{3}{x}^{\frac{3}{2}}$|${\;}_{0}^{1}$=$\frac{2}{3}$，
则b＜a＜c，
故选：C
点评 本题考查了定积分的计算，属于基础题．
练习册系列答案
相关题目
6．已知函数f（x）=|2x+1|+|2x-3|．
（1）求不等式f（x）≤6的解集；
（2）若对任意$x∈[-\frac{1}{2}，1]$，不等式f（x）≥|2x+a|-4恒成立，求实数a的取值范围．
（1）求不等式f（x）≤6的解集；
（2）若对任意$x∈[-\frac{1}{2}，1]$，不等式f（x）≥|2x+a|-4恒成立，求实数a的取值范围．
3．在△ABC中，B（-2，0），C（2，0），A（x，y），给出△ABC满足条件，就能得到动点A的轨迹方程
下表给出了一些条件及方程：
则满足条件①，②，③的轨迹方程依次为（ ）
下表给出了一些条件及方程：
| 条件 | 方程 |
| ①△ABC周长为10 | C1：y2=25 |
| ②△ABC面积为10 | C2：x2+y2=4（y≠0） |
| ③△ABC中，∠A=90° | C3：$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1（y≠0） |
| A． | C3，C1，C2 | B． | C1，C2，C3 | C． | C3，C2，C1 | D． | C1，C3，C2 |
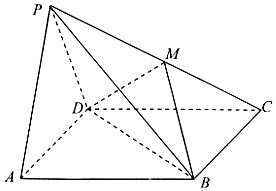如图，四棱锥P-ABCD中，底面ABCD是矩形，平面PAD⊥底面ABCD，且△PAD是边长为2的等边三角形，PC=$\sqrt{13}$，M在PC上，且PA∥面MBD．
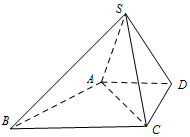如图，在底面为直角梯形的四棱锥S-ABCD中，且AD∥BC，AD=DC=1，$SA=SC=SD=\sqrt{2}$．
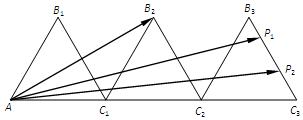如图，△AB1C1，△C1B2C2，△C2B3C3是三个边长为2的等边三角形，且有一条边在同一直线上，边B3C3上有2个不同的点P1，P2，则$\overrightarrow{A{B_2}}•（\overrightarrow{A{P_1}}+\overrightarrow{A{P_2}}）$=36．