题目内容
10.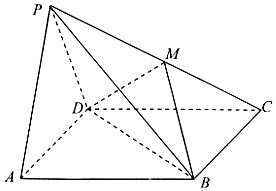 如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.(1)求证:M是PC的中点;
(2)求多面体PABMD的体积.
分析 (1)连AC交BD于E,连ME.推导出PA∥ME,由此能证明M是PC的中点.
(2)取AD中点O,连OC.则PO⊥AD,从而PO⊥面ABCD,由此能求出多面体PABMD的体积.
解答 证明:(1)连AC交BD于E,连ME.
∵ABCD是矩形,∴E是AC中点.
又PA∥面MBD,且ME是面PAC与面MDB的交线,
∴PA∥ME,
∴M是PC的中点.
解:(2)取AD中点O,连OC.则PO⊥AD,
由平面PAD⊥底面ABCD,得PO⊥面ABCD,
∴$PO⊥OC,OC=\sqrt{13-3}=\sqrt{10}$,∴$CD=\sqrt{10-1}=3$,
∴${V_{P-ABCD}}=\frac{1}{3}•2•3•\sqrt{3}=2\sqrt{3},{V_{M-BCD}}=\frac{1}{3}•\frac{1}{2}•2•3•\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{2}$,
∴${V_{PABMD}}=2\sqrt{3}-\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{3}}}{2}$.
点评 本题考查点是线段的中点的证明,考查多面体的体积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查数形结合思想、转化化归思想,是中档题.

练习册系列答案
相关题目
20.若x,y是正数,且$\frac{1}{x}+\frac{4}{y}=1$,则x+y有( )
| A. | 最小值9 | B. | 最大值9 | C. | 最小值$5+2\sqrt{2}$ | D. | 最大值$5+2\sqrt{2}$ |
5.已知a=-2${\;}^{1-lo{g}_{2}3}$,b=1-log23,c=cos$\frac{5π}{6}$,则a,b,c的大小关系是( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
15.已知a=${∫}_{0}^{1}$xdx,b=${∫}_{0}^{1}$x2dx,c=${∫}_{0}^{1}$$\sqrt{x}$dx,则a,b,c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
20.已知集合A={x|-1≤x<3},B={x∈Z|x2<4},则A∩B=( )
| A. | {0,1} | B. | {-1,0,1} | C. | {-1,0,1,2} | D. | {-2,-1,0,1,2} |
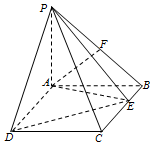 如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD为矩形,PA=AB=2,AD=4,点F是PB的中点,点E在边BC上移动.