题目内容
4.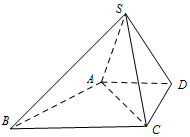 如图,在底面为直角梯形的四棱锥S-ABCD中,且AD∥BC,AD=DC=1,$SA=SC=SD=\sqrt{2}$.
如图,在底面为直角梯形的四棱锥S-ABCD中,且AD∥BC,AD=DC=1,$SA=SC=SD=\sqrt{2}$.(Ⅰ)求证:AC⊥SD;
(Ⅱ)求三棱锥B-SAD的体积.
分析 (Ⅰ)设O为AC的中点,连接OS,OD,推导出OS⊥AC,DO⊥AC,从而AC⊥平面SOD,由此能证明AC⊥SD.
(Ⅱ)三棱锥B-SAD的体积VB-SAD=VS-BAD,由此能求出结果.
解答 证明:(Ⅰ)设O为AC的中点,连接OS,OD,
∵SA=SC,∴OS⊥AC,
∵DA=DC,∴DO⊥AC,
又OS,OD?平面SOD,且OS∩DO=O,AC⊥平面SOD,
又SD?平面SOD,∴AC⊥SD.…(6分)
解:(Ⅱ)∵O为AC的中点,在直角△ADC中,DA2+DC2=2=AC2,
则$AC=\sqrt{2},OD=\frac{{\sqrt{2}}}{2}$,
在△ASC中,∵$SA=SC=\sqrt{2}$,O为AC的中点,
∴△ASC为正三角形,且$AC=\sqrt{2},OS=\frac{{\sqrt{6}}}{2}$,
∵在△SOD中,OS2+OD2=SD2,∴△SOD为直角三角形,且∠SOD=90°,
∴SO⊥OD,又OS⊥AC,且AC∩DO=O,
∴SO⊥平面ABCD.…(10分)
∴三棱锥B-SAD的体积:
VB-SAD=VS-BAD=$\frac{1}{3}×{S}_{△BAD}×SO$
=$\frac{1}{3}×\frac{1}{2}×AD×CD×SO$=$\frac{1}{3}×\frac{1}{2}×1×1×\frac{\sqrt{6}}{2}$=$\frac{\sqrt{6}}{12}$.…(12分)
点评 本题考查线线垂直的证明,考查三棱锥的体积的求法,是中档题,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知实数x、y满足$\left\{\begin{array}{l}x-y+2≥0\\ x+y≥0\\ 4x-y-1≤0\end{array}\right.$,则z=2x+y的最大值为( )
| A. | -1 | B. | $\frac{6}{5}$ | C. | 5 | D. | 6 |
15.已知a=${∫}_{0}^{1}$xdx,b=${∫}_{0}^{1}$x2dx,c=${∫}_{0}^{1}$$\sqrt{x}$dx,则a,b,c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
12.点P(0,1)到双曲线$\frac{y^2}{4}-{x^2}=1$渐近线的距离是( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | 5 |
9.若函数f(x)=ax2-bx+1(a≠0)是定义在R上的偶函数,则函数g(x)=ax3+bx2+x(x∈R)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
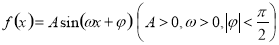 的图像过点
的图像过点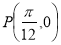 ,图像上与
,图像上与
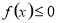 的取值范围
的取值范围