Question

周期为π的函数f（x）=2sin（ωx-

π

6

）-m（ω＞0）在x∈[0，

π

2

]上有两个零点，则实数m的取值范围为（　　）

• A、（-2，2）
• B、[1，2）
• C、[-1，2]
• D、（0，2）

Answer 1

考点：正弦函数的图象

专题：三角函数的图像与性质

分析：由f（x）=0，求得 sin（2x-

π

6

）=

m

2

．由题意可得函数y=sin（2x-

π

6

）的图象和直线y=

m

2

 在[0，

π

2

]上有两个交点，数形结合求得m的范围．

解答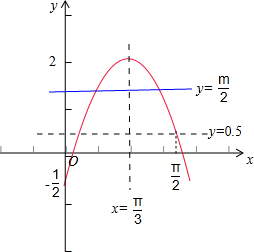： 解：由题意可得

2π

ω

=π，
∴ω=2，∴f（x）=2sin（2x-

π

6

）-m，
由f（x）=0，求得 sin（2x-

π

6

）=

m

2

．
由题意可得函数y=sin（2x-

π

6

）的图象和直线y=

m

2

 在[0，

π

2

]上有两个交点，如图所示：
故有

1

2

≤

m

2

＜1，求得 1≤m＜2，
故选：B．

点评：本题主要考查函数零点个数的应用，利用三角函数的图象是解决本题的关键，属于基础题．