题目内容
15.已知实数x,y满足$\left\{\begin{array}{l}2x+y-4≥0\\ x-y-1≤0\\ y≤3\end{array}\right.$,则z=x-3y的最大值是$-\frac{1}{3}$.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}2x+y-4≥0\\ x-y-1≤0\\ y≤3\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}{x-y-1=0}\\{2x+y-4=0}\end{array}\right.$,解得A($\frac{5}{3}$,$\frac{2}{3}$).
化目标函数z=x-3y为y=$\frac{x}{3}-\frac{z}{3}$,
由图可知,当直线y=$\frac{x}{3}-\frac{z}{3}$过A时,直线在y轴上的截距最小,z有最大值为$-\frac{1}{3}$.
故答案为:$-\frac{1}{3}$.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
3.企业需为员工缴纳社会保险,缴费标准是根据职工本人上一年度月平均工资(单位:元)的8%缴纳,某企业员工甲在2010年至2016年各年中每月所缴纳的养老保险数额y(单位:元)与年份序号t的统计如表:
(1)求y关于t的线性回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$;
(2)按照这种变化趋势,利用(1)中回归方程,预测2017年该员工每月的平均工资(精确到0.1).
参考公式和数据:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$,$\sum_{i=1}^{7}$tiyi=13860,$\sum_{i=1}^{7}$ti2=140.
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 270 | 330 | 390 | 450 | 490 | 540 | 610 |
(2)按照这种变化趋势,利用(1)中回归方程,预测2017年该员工每月的平均工资(精确到0.1).
参考公式和数据:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-b$\overline{x}$,$\sum_{i=1}^{7}$tiyi=13860,$\sum_{i=1}^{7}$ti2=140.
20.若${(x-\frac{1}{x})}^{n}$的展开式中只有第7项的二项式系数最大,则展开式中含x2项的系数是( )
| A. | -462 | B. | 462 | C. | 792 | D. | -792 |
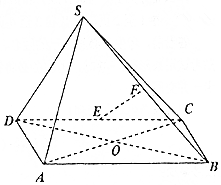 如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.
如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.